Question

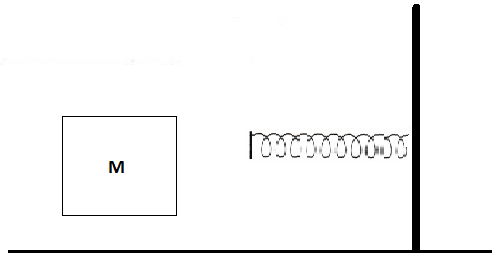
The block of mass M moving on the frictionless horizontal surface collides with a spring of spring constant K and compresses it by length L. The maximum momentum of the block after collision is:

A. Zero
B. \[\dfrac{{M{L^2}}}{K}\]
C. \[\sqrt {MK} L\]
D. \[\dfrac{{K{L^2}}}{{2M}}\]

Answer 1

Hint: In this question, we will use the principle of conservation of mechanical energy. This principle states that if only the conservative forces doing work on the body, then its mechanical energy ( kinetic energy + potential energy ) remains constant i.e. K.E + P.E = E(constant).

Complete step-by-step solution -
Formula used: K.E = $\dfrac{1}{2}m{v^2}$, P.E of stretched string = $\dfrac{1}{2}k{x^2}$, P = mv and $K.E + P.E = E({\text{constant)}}$.
We know that, if only the conservative forces are doing work on the body, then its mechanical energy ( kinetic energy + potential energy ) remains constant. It can be written as:
$ \Rightarrow K.E + P.E = E({\text{constant)}}$.
$ \Rightarrow $ $\vartriangle K + \vartriangle U = 0$
$ \Rightarrow $ $\vartriangle K = - \vartriangle U$.
If the initial velocity of the moving block is v, then the kinetic energy will be,
$ \Rightarrow K.E = \dfrac{1}{2}Mv_{\max }^2$.
As we know that the potential energy of a stretched string is $\dfrac{1}{2}k{x^2}$.
So the potential energy due to the spring is = $\dfrac{1}{2}K{L^2}$.
So now, according to the principle of conservation of energy,
Energy can neither be created nor destroyed. It may be transformed from one form to another.
So, when the spring gets compressed by length L,
K.E lost by mass M = P.E stored in the compressed spring.
$ \Rightarrow $ K.E = P.E
We have $K.E = \dfrac{1}{2}Mv_{\max }^2$ and P.E =$\dfrac{1}{2}K{L^2}$, hence
$ \Rightarrow $ $\dfrac{1}{2}Mv_{\max }^2$ =$\dfrac{1}{2}K{L^2}$.
Solving this, we get
$
   \Rightarrow v_{\max }^2 = \dfrac{{K{L^2}}}{M}. \\
   \Rightarrow {v_{\max }} = \sqrt {\dfrac{{K{L^2}}}{M}} = \sqrt {\dfrac{K}{M}} L \\
$
Now, the maximum momentum of the block,
$
   \Rightarrow {P_{\max }} = M{v_{\max }} \\
   \Rightarrow {P_{\max }} = M\sqrt {\dfrac{K}{M}} L \\
   \Rightarrow {P_{\max }} = \sqrt {MK} L \\
$
Here, we can see that the maximum momentum of the block after collision is \[\sqrt {MK} L\].
Therefore, the correct answer is option (C).

Note: In this type of question we will use the law of conservation of energy. First we have to find the initial kinetic energy and then we have to find the potential energy of the stretched string. Then by using the principle of conservation of energy, we will equate both the energies and then we will get the value of maximum velocity. And then by using that velocity we can get the value of maximum momentum.