Question

The biggest stuffed animal in the world is a snake $420m$ long, constructed by Norwegian children. Suppose the snake is laid out in a park as shown in above figure, forming two straight sides of an angle of ${105^ \circ }$, with one side $240m$ long. Olaf and Inge run a race they invent. Inge runs directly from the tail of the snake to its head, and Olaf starts from the same place at the same moment but runs along the snake.
(a) If both children run steadily at $12.0km/h$ , Inge reaches the head of the snake how much earlier than Olaf?
(b) If Inge runs the race again at a constant speed of $12.0km/h$ , at what constant speed must Olaf run to reach the end of the snake at the same time as Inge?

Answer 1

Hint: For the first part of the question, let, the tail of the snake is along the x-axis. Then, find the displacement from tail to head of the snake and thereafter, calculate the time taken by each child, using the formula, speed = distance/time. And, for the second part, using the same formula of velocity, find the speed of Olaf, if he must reach the end of the snake at the same time as Inge.

Complete step by step answer:

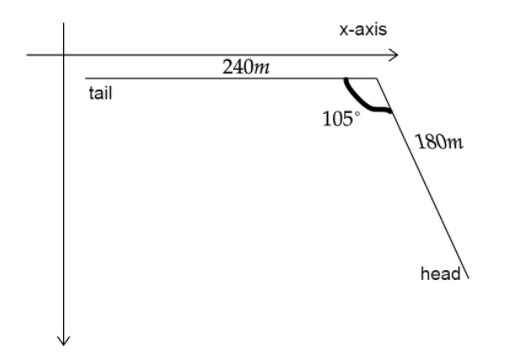
When the snake is laid out in a park forming two straight sides of an angle of ${105^ \circ }$, then one side is $240m$ long. Therefore, length of another side is-
$ = (420 - 240)m$
$ = 180m$ .
Now, take the x-axis along the tail of the snake.
So, the displacement from the tail of the snake to its head will be,
$(240m)\hat i + 180m\{ \cos ({180^ \circ } - {105^ \circ })\} \hat i - 180m(\sin {75^ \circ })\hat j$
$ = (240 + 180 \times 0.2588)m\hat i - (180 \times 0.9659)m\hat j$
$ = 287m\hat i - 174m\hat j$ ,(taking the values approximately)
And, the magnitude of this, is-
$\sqrt {{{(287)}^2} + {{(174)}^2}} m$
$ = 355m$
As, we know, speed = distance/time, so, the time required for each child’s run is –
For Inge:
$\Delta t = \dfrac{d}{v}$
$ = \dfrac{{335m(h)(1km)(3600s)}}{{(12km)(1000m)(1h)}}$
$ = 101s$
For Olaf:
$\Delta t = \dfrac{{420m.s}}{{3.33m}}$
$ = 126s$ .
Therefore, Inge reaches the head of the snake $(126 - 101)s = 25s$ earlier than Olaf.
So, for the part (a), the correct answer is $25s$ .
Now, for the part (b),
We have, Olaf has to reach the end of the snake at the same time as Inge, when Inge runs the race at a constant speed of $12.0km/h$
Let, Olaf must run at the constant speed $v$ $km/h$ .
Therefore, using the formula, $v = \dfrac{d}{{\Delta t}}$ , we get,
$v = \dfrac{{420m}}{{101s}}\left( {\dfrac{{3600s}}{{1h}}} \right)\left( {\dfrac{{km}}{{{{10}^3}m}}} \right)$
$ = 15.0km/h$ .
So, Olaf must run the race at constant speed $15km/h$ to reach the end of the snake at the same time as Inge, when Inge runs at a constant speed of $12km/h$ .

Hence, the correct answer is option (B).

Note: For part (a), we know, magnitude of a vector $\vec a = {a_1}\hat i + {a_2}\hat j + {a_3}\hat k$ is, $a = \sqrt {{a_1}^2 + {a_2}^2 + {a_3}^2} $ . Using this formula, we have found the magnitude of the displacement from the tail of the snake to its head. And, in both parts, speed is calculated from the definition, ‘the time rate of change of distance is known as speed’.