Question

The base of the right prism is a right angled triangle. The measure of the base of the right angled triangle is 3m and its height 4m. If the height of the prism is 7m then find
A.The member of edges of the prism
B.The volume of the prism.
C.The total surface area of the prism.

Answer 1

Hint : Same formulas to keep in mind while sowing the question of prism are,
The member of the edges of the prism =member of sides of the base $ \times 3.$
Second one is, the volume of the prism is = area of the base multiplied by the height of the prism.
The total surface area is equal to lateral surface area $ + 2$ (base area).

Complete step-by-step answer:
In the question we are given that the measure of the base of the triangle $ = 3m$
The height of the triangle $ = 4m$
$\therefore $ The hypotenuse of the right angled triangle $ = \sqrt {{3^2} + {4^2}} \;\; = \sqrt {25} = 5$.
The height of the prism $ = 7m$

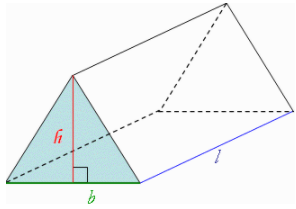
Now let's apply the formula mentioned above,
1). No of edges $ = $ no. of sides of the base $ \times 3$
               $ = 3 \times 3 = 9\;\;\;\;\;\;\;\;\;\;\left[ {\because {\text{base}}\;{\text{is}}\;{\text{a}}\;{\text{triangle}}} \right]$
2). The volume of the prism = Area of base $ \times $ Height of prism
                    $ = \dfrac{1}{{{2}}}\left( {3 \times 4} \right) \times 7$
                    $ = 6 \times 7 = 42{m^{3\;\;\;\;\;}}\,\;\;\;\;\;\;\;\;\;\;\;\;\;\;\;\left[ {\because \;{\text{area}}\;{\text{of}}\;{\text{triangle}}\; = \dfrac{1}{2}\left( {{{base \times height}}} \right)} \right]$
3). Total surface area = lateral
     Surface area$ + 2$ (area of base)
                    $ = \;{\text{ph}}\;{\text{ + 2}}$ (area of base)
$\left[ {{\text{where}}\;{\text{p}}\;{\text{ = }}\;{\text{perimeter}}\;{\text{of}}\;{\text{base}}} \right]$
$\left[ {{\text{h}}\;{\text{ = }}\;{\text{height}}\;{\text{of}}\;{\text{prism}}} \right]$
$ = \left( {3 + 4 + 5} \right).7 + 2.\left( 6 \right)$
$ = 84 + 12$
$ = 96{m^2}.$

Note : In geometry questions we should always try to visualize the figure in our mind, so that we can link the formula clearly with it and then the chances of forgetting the formula reduces.