Answer
Verified453.9k+ views
Hint: We know that in geometry, an equilateral triangle is a triangle in which all three sides are equal. We all are familiar with the Euclidean geometry that says, an equilateral triangle is also equiangular; that is, all three internal angles are also congruent to each other and are each 60°. It is also a regular polygon, so it is also referred to as a regular triangle.
We know that the equation of a line is with one known point and the slope of line given is as follows:
\[\dfrac{y-b}{x-a}=m\]
(Where m is the slope of the line and (a, b) is the known point that lies on the line)
Complete step by step answer:
As given in the question, we have to find the 3 vertices of the given equilateral triangle.
Now, as the mid-point of the base of the equilateral triangle is the origin (0, 0) and as the side of the equilateral triangle is given as 2a. It is also given that both the endpoints lie on the y-axis. Hence, by symmetry we can say that these two vertices have the coordinates (0, a) and (0, -a).
Now, as we know that, all the angles of an equilateral triangle are equal to 60°.
So, the equation of the line that is one side of the equilateral triangle and which is having (0, -a) point and the third vertex can be written as follows:
\[\begin{align}
& \dfrac{y-(-a)}{x-0}=\tan {{30}^{\circ }} \\
&\Rightarrow y+a=x\dfrac{1}{\sqrt{3}} \\
&\Rightarrow \sqrt{3}\left( y+a \right)=x \\
\end{align}\] Since, $slope=\tan \theta $
Now, from the concept of symmetry, we can say that the third vertex also lies on the x-axis, so, we will place$y=0$,
\[\begin{align}
& \sqrt{3}\left( y+a \right)=x \\
&\Rightarrow \sqrt{3}a=x \\
\end{align}\]
Hence, the third vertex is
\[\left( \sqrt{3}a,0 \right)\] .
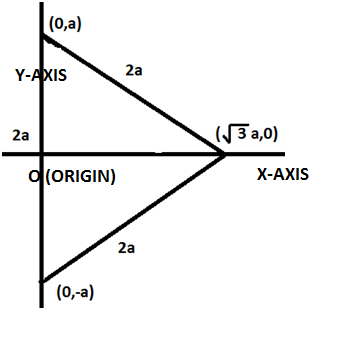
Hence, $\left( \sqrt{3}a,0 \right),\left( 0,a \right),\left( 0,-a \right)$ are the coordinates of the three vertices of the equilateral triangle.
Note: We can make an error if we don’t know the formula to get the slope of a line that is,
The equation of a line is with one known point and the slope of line given is as follows:
\[\dfrac{y-b}{x-a}=m\]
(Where m is the slope of the line and (a, b) is the known point that lies on the line)
Also, assessing the question that the midpoint of one side of the equilateral triangle will be the origin is very essential as without this information, one can never get to the correct answer.
We know that the equation of a line is with one known point and the slope of line given is as follows:
\[\dfrac{y-b}{x-a}=m\]
(Where m is the slope of the line and (a, b) is the known point that lies on the line)
Complete step by step answer:
As given in the question, we have to find the 3 vertices of the given equilateral triangle.
Now, as the mid-point of the base of the equilateral triangle is the origin (0, 0) and as the side of the equilateral triangle is given as 2a. It is also given that both the endpoints lie on the y-axis. Hence, by symmetry we can say that these two vertices have the coordinates (0, a) and (0, -a).
Now, as we know that, all the angles of an equilateral triangle are equal to 60°.
So, the equation of the line that is one side of the equilateral triangle and which is having (0, -a) point and the third vertex can be written as follows:
\[\begin{align}
& \dfrac{y-(-a)}{x-0}=\tan {{30}^{\circ }} \\
&\Rightarrow y+a=x\dfrac{1}{\sqrt{3}} \\
&\Rightarrow \sqrt{3}\left( y+a \right)=x \\
\end{align}\] Since, $slope=\tan \theta $
Now, from the concept of symmetry, we can say that the third vertex also lies on the x-axis, so, we will place$y=0$,
\[\begin{align}
& \sqrt{3}\left( y+a \right)=x \\
&\Rightarrow \sqrt{3}a=x \\
\end{align}\]
Hence, the third vertex is
\[\left( \sqrt{3}a,0 \right)\] .
Hence, $\left( \sqrt{3}a,0 \right),\left( 0,a \right),\left( 0,-a \right)$ are the coordinates of the three vertices of the equilateral triangle.
Note: We can make an error if we don’t know the formula to get the slope of a line that is,
The equation of a line is with one known point and the slope of line given is as follows:
\[\dfrac{y-b}{x-a}=m\]
(Where m is the slope of the line and (a, b) is the known point that lies on the line)
Also, assessing the question that the midpoint of one side of the equilateral triangle will be the origin is very essential as without this information, one can never get to the correct answer.