Question

The base of a triangular field is three times its height. If the cost of cultivating the field is Rs 1080 per hectare. If the total cost of cultivating the field is Rs 14580. Find its base and height.

Answer 1

Hint: Use unitary method to find the area of triangular field by dividing the total cost of cultivating the field by cost of cultivation per hectare. Equate the area obtained with the formula of the area of the triangle. Use the relation between the base and height of the triangular field to solve for the height of the triangular field.
* Area of triangle=$\dfrac{1}{2} \times b \times h$ where b=base of a triangle and h=height of a triangle

Complete step-by-step answer:
 Let ABC is a triangle whose base is BC and through point A draw a perpendicular line to side BC at point D, such that AD becomes the height of a triangle.

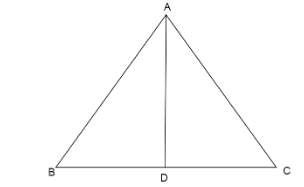
Given: - BC=3AD (Base of triangular field is three times its height)
Cost of cultivating the field per hectare= Rs 1080
Total cost of cultivating the field= Rs 14580
Therefore area of triangular field=Total cost of cultivating the field/Cost of cultivating the field per hectare
$ \Rightarrow \dfrac{{14580}}{{1080}} = 13.5$
Hence area of triangular field=13.5 hectare
Now applying the conversion of hectare into metre i.e. 1 hectare=10000square meter
\[ \Rightarrow 13.5 \times 10000 = 135000\]Square meter
Now we know that the area of the triangle=$\dfrac{1}{2} \times b \times h$ where b=base of a triangle and h=height of a triangle.
Area of triangle=$\dfrac{1}{2} \times BC \times AD$
$ \Rightarrow \dfrac{1}{2} \times 3AD \times AD$ (Given: - BC=3AD (Base of triangular field is three times its height)
$ \Rightarrow \dfrac{1}{2} \times 3A{D^2} = 135000$
$ \Rightarrow 3A{D^2} = 135000 \times 2$ (Cross multiplying)
$ \Rightarrow A{D^2} = \dfrac{{135000 \times 2}}{3}$
$ \Rightarrow A{D^2} = 90000$
$ \Rightarrow AD = \sqrt {90000} $
$\therefore AD = 300$Meter
Therefore the height of a triangular field is 300 meter.
Now as it is given BC=3AD. So, $BC = 3 \times 300 = 900$Meter
Therefore the base of a triangular field is 900 meter.

Note: Students may likely make mistakes by directly taking an area of triangular field in hectares but that is not the correct way of solving rather all units should be converted into standard units.