Question

The base of a triangle is $4$ cm greater than the height. The area is $30c{m^2}$ . How do you find the height and the length of the base?

Answer 1

Hint: The first step on how to find the height of a triangle is by recalling the formula for the area of a triangle.
The formula for the area of a triangle is $A = \dfrac{1}{2} \times b \times h$ . \Where A = Area of the triangle, b = Length of the base of the triangle, h = Height of the base of the triangle.
Look at the triangle to find out what factors you know. Plug the values into the equation and do the calculations.
The resulting value will be your triangle height!

Complete step-by-step solution:
We know the area of a triangle whose base $b$ and height $h$ is $\dfrac{1}{2} \times b \times h$

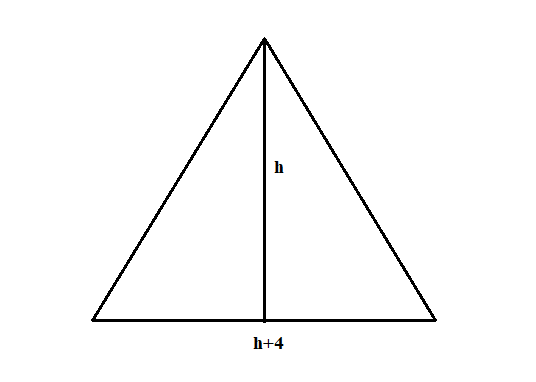
Let the height of given triangle be $h\,$ cm and as base of a triangle is $4$ cm greater than the height
Therefore base is $\left( {h + 4} \right)$.
Now substitute the values in the Area formula
Hence, its area is $\dfrac{1}{2} \times h \times \left( {h + 4} \right)$ and this is $30\,c{m^2}$.
 So $\dfrac{1}{2} \times h \times \left( {h + 4} \right) = 30$
Now reducing the equation by multiplying inside brackets
$ \Rightarrow {h^2} + 4h = 60$
On rewriting the term and we get
$ \Rightarrow {h^2} + 4h - 60 = 0$
Now by separating the equation we get
$ \Rightarrow {h^2} + 10h - 6h - 60 = 0$
Taking the common term and we get
$ \Rightarrow h\left( {h + 10} \right) - 6\left( {h + 10} \right) = 0$
On rewriting we get
$ \Rightarrow \left( {h - 6} \right)\left( {h + 10} \right) = 0$
Therefore we get
$ \Rightarrow h = 6\,$ and $h = - 10$
But height of triangle cannot be negative
Therefore the height of a triangle is $h = 6$
Base=$\left( {h + 4} \right) = \left( {6 + 4} \right) = 10$ cm.

Therefore the base and height of the triangle is $10$cm and $6$cm.

Note: Find the Height of a Triangle by Finding an Equilateral Triangle's Height:
An equilateral triangle has three equal sides and three equal $60$ degree angles. When you cut in half an equilateral triangle, you end up with two congruent right triangles.
The Pythagorean Theorem states that for any right triangle of length sides $a$ and $b$, and length hypotenuse $c:$ ${a^2} + {b^2} = {c^2}$ We can use the theorem to calculate our equilateral triangle's height!
Split the triangle equilaterally and add values to variables $a$ , $b$ , and $c$. The hypotenuse $c$ would be equal to the length of the original side. Side a would be equal to $\dfrac{1}{2}$ the length of the side, and side $b$ is the height of the triangle we will solve.
Plug the values into the theorem of Pythagorean and solve ${b^2}$ . First square $c$ and $a$ to add every number by themselves. Subtract from ${c^2}$ then ${a^2}$.
To get the height of the triangle, consider the square root of ${b^2}$. To find square roots using the square root feature on your calculator. The result is the height of the equilateral triangle.