Question

The base of a prism is a right angled triangle with legs 6cm, 8cm, and hypotenuse 10cm. If the total surface area of the prism is 156cm2, find its height and its lateral surface area.

Answer 1

Hint: Find the different shapes which a prism is composed of and then calculate their areas by assuming the height of the prism. Add all the areas and equate it to the area given in question. This shall give the height and after getting the height calculate the lateral surface area.

Complete step-by-step solution:
A prism is a polyhedron having 2 same n-sided polygonal bases and n-other rectangular faces joining corresponding sides of the two bases. The rectangular faces are also called as the lateral faces and the sum of their areas is the lateral surface area.
A triangular prism has 2 triangular faces and 3 rectangular faces.
The triangles are right angled so, their area becomes $\dfrac{1}{2} \times b \times h$ which is $\dfrac{{1 \times 6 \times 8}}{2} = 24$
For 2 triangular faces, we have the area 48 $\text{cm}^2$.
Now, let's assume the height of the prism as h.
The sum of the area of the 3 rectangular faces will give us the lateral surface area.
So, the 3 rectangles will have h as length and the edge of the triangle as the other on edge that is the width.

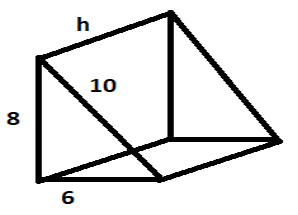
The area of the rectangles will then be computed as h $ \times $6, h $ \times $8, h $ \times $10.
The lateral surface area= $h \times (6 + h)\times (8 + h)\times 10$ = $ h\times (6+8+10)$ = $h\times (24)$
We know that the sum of the two triangular faces and the lateral surface area of the prism will give us the total surface of the prism. So,
48 + h $ \times $(24) = 156 (as given in question)
H $ \times $24 = 108
$h = \dfrac{9}{2}$
And the lateral surface area becomes 108 $\text{cm}^2$.

Note- In order to do this question, one should know the meaning of the terms used in the question and also the definition of a prism in order to remember the shape and solve the question.