Question

The base of a parallelogram is twice its height. If the area of the parallelogram is 72 sq. cm, find its height.

Answer 1

Hint: We will assume the height and base of the parallelogram to be \[x\]cm and \[2x\] cm respectively. We will substitute these values in the formula for the area of a parallelogram and equate it to 72. We will simplify the equation and find the height of the parallelogram.
Formulas used: We will use the formula of the area (A) of a parallelogram is given by \[A = b \times h\] where \[b\] is the height of the parallelogram and \[h\] is the height of the parallelogram.

Complete step by step solution:
We will assume that the height of the parallelogram is \[x\] cm.
\[h = x\]
We know that the base of the parallelogram is twice the height of the parallelogram. So, the base \[b\] of the parallelogram will be \[2x\] cm :
\[b = 2x\]
We know that the area of the parallelogram is 72 sq. cm. We will substitute 72 for A, \[2x\] for \[b\] and \[x\] for \[h\] in the formula for the area of a parallelogram:
\[72 = 2x \cdot x\\ \Rightarrow 72 = 2{x^2}\]
We will divide both sides of the equation by 2:
\[ \Rightarrow \dfrac{{72}}{2} = \dfrac{{2{x^2}}}{2}\\ \Rightarrow 36 = {x^2}\]
We will take square root on both sides of the equation:
\[ \Rightarrow \sqrt {36} = \sqrt {{x^2}} \\ \Rightarrow 6 = x\]
$\therefore $ The height of the parallelogram is 6 cm.

Note: A parallelogram is any 4 sided figure whose opposite sides are parallel and equal to each other. A rectangle is a special case of a parallelogram where adjacent sides are perpendicular to each other:

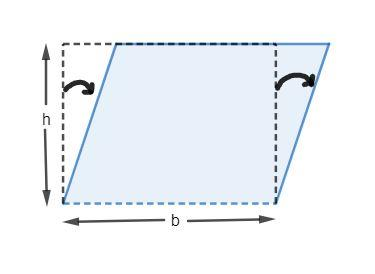
A square is a special case of a rectangle (and thus a parallelogram) where all sides are equal and all angles are also right angles.
A rhombus is also a special case of a parallelogram where all sides are equal but the angles are not right angles.