Question

The base and height of a triangle are in the ratio \[3:2\] and its area is \[108c{{m}^{2}}\]. Find its base and height?

Answer 1

Hint: We know that the area of a triangle is equal to \[\dfrac{1}{2}bh\] where b is length of base of triangle and h is height of triangle. The height of a triangle is perpendicular to the base of the triangle. In the same way, we can calculate the base of triangle if area of triangle and height of triangle is known and we can also calculate the height of triangle if area if triangle and base of triangle is known.

Complete step-by-step solution -
Before solving the question, we should know that the area of a triangle is equal to \[\dfrac{1}{2}bh\] where b represents length of base of triangle and h represents height of triangle. In the question, it was given that the ratio of base and height of the triangle is \[3:2\] and also the area of the triangle is \[108c{{m}^{2}}\].
 

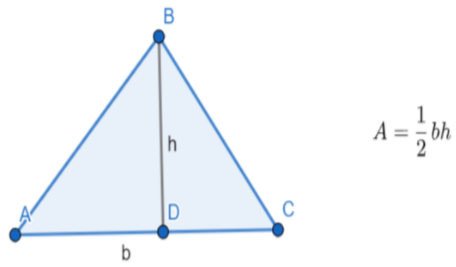
The formulae of the area of \[\Delta ABC\] is illustrated in the above diagram.
Let us assume the base of the triangle is b, height of the triangle is h and area of the triangle is A.
We know that the ratio of base and height of the triangle is \[3:2\].
\[\begin{align}
  & \Rightarrow b:h=3:2 \\
 & \Rightarrow \dfrac{b}{h}=\dfrac{3}{2} \\
\end{align}\]
By cross multiplication,
\[\Rightarrow b=\dfrac{3h}{2}......(1)\]
We know that the area of a triangle is equal to \[\dfrac{1}{2}bh\] where b represents length of base of triangle and h represents height of triangle.
From equation (1)
\[\begin{align}
  & \Rightarrow A=\dfrac{1}{2}bh \\
 & \Rightarrow A=\dfrac{1}{2}\left( \dfrac{3h}{2} \right)\left( h \right) \\
 & \Rightarrow A=\dfrac{3{{h}^{2}}}{4}.....(2) \\
\end{align}\]
We know that the area of the triangle is \[108c{{m}^{2}}\].
From equation (2),
\[\Rightarrow \dfrac{3{{h}^{2}}}{4}=108\]
By cross multiplication,
\[\begin{align}
  & \Rightarrow 3{{h}^{2}}=4(108) \\
 & \Rightarrow 3{{h}^{2}}=432 \\
 & \Rightarrow {{h}^{2}}=\dfrac{432}{3} \\
 & \Rightarrow {{h}^{2}}=144 \\
 & \Rightarrow h=12cm.....(3) \\
\end{align}\]
Substitute equation (3) in equation (1)
\[\begin{align}
  & \Rightarrow b=\dfrac{3(12)}{2} \\
 & \Rightarrow b=\dfrac{36}{2} \\
 & \Rightarrow b=18cm......(4) \\
\end{align}\]
From equation (3) and equation (4), we get the value of h is equal to 12 cm and the value of b is equal to 12cm.
Hence, the height of the triangle is 12 cm and the base of the triangle is 18 cm.

Note: We can also calculate the area of the triangle of sides a, b and c through another formulae. \[Area=\sqrt{s(s-a)(s-b)(s-c)}\] where s is semi-perimeter of triangle and a, b and c are sides of triangle. All the formulae for the area of the triangle represents the same. One formula can be obtained from another formula.