Question

The barrel of a fountain pen, cylindrical in shape, is $7$cm long and $5$mm in diameter. A full barrel of ink in the pen will be used up on writing $330$ words on an average. How many words would use up a bottle of ink containing one fifth of litre?
A) $60000$
B) $66000$
C) $48000$
D) $50000$

Answer 1

Hint:
First, convert the unit mm into cm. Then find the volume of the barrel using the formula of the volume of cylinder which is given as-
$ \Rightarrow $ Volume of cylindrical barrel=$\pi {r^2}h$ where r= radius and h=height
Put the given values and solve. Then change the unit litre into cubic cm and find the volume of the ink used. Then find the number of word used to write $330$ words using a bottle of ink containing one fifth of litre($\dfrac{{1000}}{5}{\text{c}}{{\text{m}}^3}$ ).

Complete step by step solution:
Given, a barrel of a fountain pen is cylindrical in shape. It is $7$cm long and $5$mm in diameter. A full barrel of ink in the pen will be used up on writing $330$ words. We have to find the number of words to be written to use up a bottle of ink containing one fifth of litre.
Since the barrel is in cylindrical shape so we can draw the figure as-

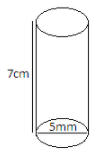
First we will find the volume of the cylindrical barrel. We know that the volume of cylinder is given as-
$ \Rightarrow $ Volume of cylindrical barrel=$\pi {r^2}h$ where r= radius and h=height
Now, according to the figure h=$7$cm and diameter=$5$mm
We know that $1{\text{mm = }}\dfrac{{\text{1}}}{{{\text{10}}}}{\text{cm}}$ so diameter=$\dfrac{5}{{10}}$ cm
Now we know that r=half of the diameter
$ \Rightarrow r = \dfrac{5}{{10}} \times \dfrac{1}{2}$
On solving, we get-
$ \Rightarrow r = \dfrac{1}{4}$ cm
We also know that $\pi = \dfrac{{22}}{7}$
On putting the given values in the formula, we get-
$ \Rightarrow $ Volume of cylindrical barrel=$\dfrac{{22}}{7} \times {\left( {\dfrac{1}{4}} \right)^2} \times 7$
On solving, we get-
$ \Rightarrow $ Volume of cylindrical barrel=$22 \times \dfrac{1}{4} \times \dfrac{1}{4}$
On solving further, we get-
$ \Rightarrow $ Volume of cylindrical barrel=$\dfrac{{11}}{8}$
On dividing, we get-
$ \Rightarrow $ Volume of cylindrical barrel=$1.375{\text{ c}}{{\text{m}}^3}$ -- (i)
The given volume of ink in the bottle is one fifth of litre.
We know that $1$ Litre=$1000{\text{ c}}{{\text{m}}^3}$
Then the given volume of ink in the bottle=$\dfrac{1}{5} \times 1000{\text{ c}}{{\text{m}}^3}$
On solving, we get-
The given volume of ink in the bottle=$200{\text{ c}}{{\text{m}}^3}$-- (ii)
This means that $1.375{\text{ c}}{{\text{m}}^3}$ink is used in writing the number of words=$330$
So $1{\text{ c}}{{\text{m}}^3}$ ink is used to write the number of words=$\dfrac{{330}}{{1.375}}$
Then ${\text{200 c}}{{\text{m}}^3}$ ink is used to write the number of words=$\dfrac{{330}}{{1.375}} \times 200$
On solving, we get-
$ \Rightarrow {\text{200 c}}{{\text{m}}^3}$ ink is used to write the number of words=$240 \times 200$
On multiplication, we get-
$ \Rightarrow {\text{200 c}}{{\text{m}}^3}$ ink is used to write the number of words=$48000$

Answer- The correct answer is option C.

Note:
The student may go wrong if they forget to notice that the volume of ink in the bottle is already given in the question and they do not convert the unit of the Volume of ink In the bottle to centimeter as it is the only tricky part in the question.