Question

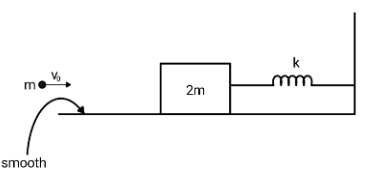
The ball of mass $m$ is thrown with speed ${v_0}$. The ball strikes the block of mass $2m$ and sticks to it. Find the maximum compression of spring.

(A) ${v_0}\sqrt {\dfrac{m}{{3k}}} $
(B) ${v_0}\sqrt {\dfrac{m}{{2k}}} $
(C) ${v_0}\sqrt {\dfrac{{2m}}{k}} $
(D) ${v_0}\sqrt {\dfrac{{3m}}{k}} $

Answer 1

Hint:Here, you are given a block which is connected to a spring and the other end of the spring is connected to the wall. A ball of mass of mass $m$ is thrown on that block and sticks. Just before the ball hits the block, its velocity is ${v_0}$, no after the collision, the block and ball will have a common velocity and will reach at maximum compression together because it is given that the ball sticks the block. You need to find the common velocity and then you can apply the work energy theorem in order to find the maximum compression. The only crucial part you need to focus on is how to get that common velocity of the ball and block.

Complete step by step answer:
The only way to find the common velocity of the ball and block system is to apply the conservation of momentum. The momentum should be conserved just before and just after the collision. Now, you might be thinking that why is the momentum conservation law used here? There is already a spring force that will be acting on the block that will be restricting us to use the momentum conservation.

The answer is yes, it is restricting but still we can apply it. Because the force of spring depends on the elongation or compression of the spring, how much it is elongated or compressed. Initially, just after the collision, the block and ball will move with some common velocity, say $v$ but notice that the compression produced will be infinitesimally small and so will be the force due to spring. So, the force due to spring can be neglected and therefore, we can apply momentum conservation. Hence, we get the common velocity as follows
$m{v_0} = \left( {m + 2m} \right)v \\
\Rightarrow v = \dfrac{{{v_0}}}{3} \\ $
Now, apply the work energy theorem. If the maximum compression is ${x_{\max }}$, we have
$- \dfrac{1}{2}k{\left( {{x_{\max }}} \right)^2} = 0 - \dfrac{1}{2}3m{v^2} \\
\Rightarrow\dfrac{1}{2}k{\left( {{x_{\max }}} \right)^2} = \dfrac{{3m}}{2}{\left( {\dfrac{{{v_0}}}{3}} \right)^2} \\
\therefore{x_{\max }} = {v_0}\sqrt {\dfrac{m}{{3k}}} \\ $
Therefore, the maximum compression of spring is ${v_0}\sqrt {\dfrac{m}{{3k}}} $ and option A is correct.

Note:We have used momentum conservation regardless of whether the spring is applying a force on the system or not because the force is too small that it can be neglected and the whole momentum which was carried by the ball initially is transferred to the ball and block system. Remember the work energy theorem. Also notice that the interval in which the work energy theorem is applied is the interval where the block and ball start moving together after the collision till the maximum compression.