Question

The area of triangle formed by the tangents from point (3,2) to hyperbola ${{x}^{2}}-9{{y}^{2}}=9$ and the chord of contact w.r.t. point (3,2) is :

Answer 1

Hint: Start by finding the equation of the chord of contact followed by the points where the chord of contact meets the hyperbola. Now once you know the points, you know all the three vertices of the triangle, so use the formula of area of the triangle with given vertices to get the answer.

Complete step by step solution:
First let us write the equation of hyperbola in standard form. On doing so, we get
${{x}^{2}}-9{{y}^{2}}=9$
$\Rightarrow \dfrac{{{x}^{2}}}{9}-{{y}^{2}}=1$
Let us start by drawing a representative diagram of the situation given in the figure.

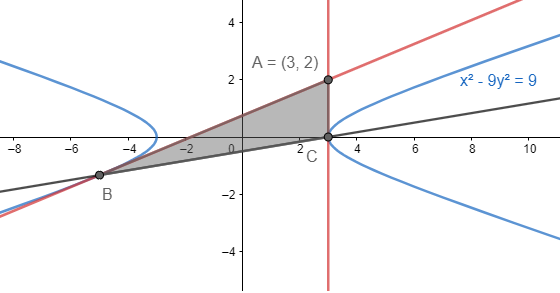
Now we know that one of the vertices of the triangle is (3,2). We also know that the chord of contact to the hyperbola $\dfrac{{{x}^{2}}}{{{a}^{2}}}-\dfrac{{{y}^{2}}}{{{b}^{2}}}=1$ w.r.t. point (p,q) is given by $\dfrac{px}{{{a}^{2}}}-\dfrac{qy}{{{b}^{2}}}=1$ . So, the chord of contact given in the question is:
$\dfrac{3x}{9}-2y=1$
$\Rightarrow x=3\left( 2y+1 \right)............(i)$
Now, if we solve the equation of chord of contact with the equation of hyperbola, the points we get are the other two vertices of the triangle. So, substituting x from equation (i) in equation of hyperbola, we get
$\dfrac{9{{\left( 2y+1 \right)}^{2}}}{9}-{{y}^{2}}=1$
We know that ${{\left( a+b \right)}^{2}}={{a}^{2}}+{{b}^{2}}+2ab$ .
$4{{y}^{2}}+1+4y-{{y}^{2}}=1$
$\Rightarrow 3{{y}^{2}}+4y=0$
$\Rightarrow y\left( 3y+4 \right)=0$
So, the possible values of y are 0 and $-\dfrac{4}{3}$ .
If we put y=0 in equation (i), we get x=3. Also, if we put y to be $-\dfrac{4}{3}$ , we get x=-5.
So, the vertices of the triangle are (3,2), (3,0) and $\left( -5,-\dfrac{4}{3} \right)$ .
Now we know that the area of the triangle is equal to the absolute value of:
$\dfrac{1}{2}\left| \begin{matrix}
   1 & {{x}_{1}} & {{y}_{1}} \\
   1 & {{x}_{2}} & {{y}_{2}} \\
   1 & {{x}_{3}} & {{y}_{3}} \\
\end{matrix} \right|=\dfrac{1}{2}\left| \begin{matrix}
   1 & 3 & 2 \\
   1 & 3 & 0 \\
   1 & -5 & \dfrac{-4}{3} \\
\end{matrix} \right|=\dfrac{1}{2}\left( 1\left( -4-0 \right)-1\left( -4+10 \right)+1\left( 0-6 \right) \right)=-8$
So, the answer to the above question is 8sq units. Area is not to be negative and write it as |-8|.

Note: You could have also solved the questions by finding the tangents and the chord of contact, but that would be lengthy and complex to solve. Also, you need to learn all the formulas related to standard conic sections as they are used very often.