Question

The area of the shaded region in the figure is,

$
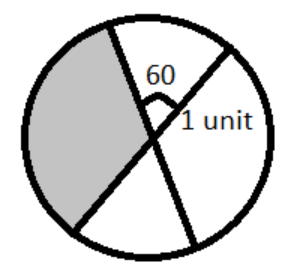
  A.\dfrac{\pi }{3} \\
  B.\dfrac{\pi }{2} \\
  C.\dfrac{\pi }{4} \\
  D.{\pi ^2} \\
$

Answer 1

Hint: In order to solve this problem we need to get the angle made by line in a shaded region with the help of a given angle of 60 degrees and then we will find the area dividing the area of the whole circle with respect to angle and get the right answer to this problem.

Complete step-by-step answer:
We need to find the area of the shaded region then.
So, the angle present in the shaded region is 120 degrees.
This is because the angle of line is of 180 degrees and 60 degrees is made by other parts of the line, so the other part will be of 120 degrees since the sum of all angles must be 180 degrees in a line.
This could be the figure after assigning the angle.

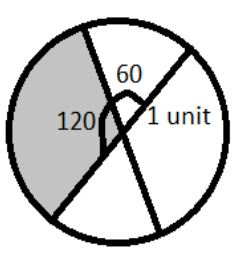
Area of the shaded region will be calculated with the help of angle 120 degrees.
Since the area of the circle of radius r is $\pi {r^2}$ that time the angle is whole 360 degrees.
But when we need to calculate the area of the 120 degrees part then we have to multiply the area with $\dfrac{{120}}{{360}}$ degrees.
So, the area of the shaded region is,
$ \Rightarrow \pi {r^2} \times \dfrac{{120}}{{360}} \\
   \Rightarrow \pi {\left( 1 \right)^2}\dfrac{1}{3} = \dfrac{\pi }{3} $
Hence, the area of the shaded region is $\dfrac{\pi }{3}$.
So, the correct option is A.

Note: In such problems of finding the area of any part of the circle you need to know the angle subtended at the centre to get the area by the above method. If we have the arc length of that part and the radius then also we can find the angle with the formula angle in radians is equal to arc length upon the radius of the circle. Then you can find the area of that part of the circle. Doing this will solve your problem and will give you the right answer.