Question

The area of the rhombus is \[480c{{m}^{2}}.\] If one of the diagonals is 32 cm, find the other.

Answer 1

Hint: To solve the given question, we will first find out what a rhombus is. Then we will draw a rhombus whose each side is x and we will divide it into two triangles. Now, the area of one triangle will be half of the rhombus.
Then we will find the angle between two sides by the formula \[\cos A=\dfrac{{{b}^{2}}+{{c}^{2}}-{{a}^{2}}}{2bc},\] then we will apply the area of the triangle as \[\dfrac{1}{2}bc\sin A\] and equate it to the half of area of the rhombus. From here, we will get the length of a side x. Then we will calculate the angle between the two sides. After that, we will draw another diagonal. Now, we will apply Pythagora's theorem in the right-angled triangle formed and from here, we will calculate the length of other diagonal.

Complete step-by-step answer:
Before we solve the question given, we must know the rhombus is. A rhombus is a special type of parallelogram in which all the sides are equal. Let us assume that the rhombus given in the question has each side x as shown in the figure.

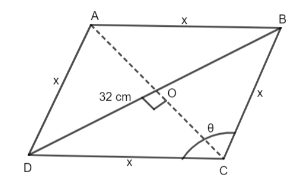
Now, BD is diagonal with length 32 cm and it divides the rhombus into two triangles of equal area. So, we can say that,
\[\text{Area of ABCD}=2\times \text{ Area of }\Delta \text{BCD}\]
In the question, it is given that the area of ABCD is \[480c{{m}^{2}}.\]
\[480c{{m}^{2}}=2\times \text{ Area of }\Delta \text{BCD}\]
\[\Rightarrow \text{Area of }\Delta \text{BCD}=240c{{m}^{2}}......\left( i \right)\]
Now, we will find the angle \[\theta \] in terms of x. We know that, in triangle PQR,
\[\cos P=\dfrac{{{q}^{2}}+{{r}^{2}}-{{p}^{2}}}{2qr}\]
Thus, in triangle BCD, we have,
\[\cos \theta =\dfrac{{{x}^{2}}+{{x}^{2}}-{{\left( 32 \right)}^{2}}}{2{{x}^{2}}}\]
\[\Rightarrow \cos \theta =\dfrac{2{{x}^{2}}-1024}{2{{x}^{2}}}\]
\[\Rightarrow \cos \theta =\dfrac{{{x}^{2}}-512}{{{x}^{2}}}......\left( ii \right)\]
Now, we know that, \[{{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1.\] Thus, \[\sin \theta =\sqrt{1-{{\cos }^{2}}\theta }.\] Thus, we have,
\[\sin \theta =\sqrt{1-{{\cos }^{2}}\theta }.....\left( iii \right)\]
From (ii) and (iii), we have,
\[\Rightarrow \sin \theta =\sqrt{1-{{\left( \dfrac{{{x}^{2}}-512}{{{x}^{2}}} \right)}^{2}}}\]
\[\Rightarrow \sin \theta =\sqrt{1-\dfrac{{{\left( {{x}^{2}}-512 \right)}^{2}}}{{{x}^{4}}}}\]
\[\Rightarrow \sin \theta =\dfrac{\sqrt{{{x}^{4}}-{{\left( {{x}^{2}}-512 \right)}^{2}}}}{{{x}^{2}}}\]
\[\Rightarrow \sin \theta =\dfrac{\sqrt{{{x}^{4}}-\left( {{x}^{4}}-1024{{x}^{2}}+{{\left( 512 \right)}^{2}} \right)}}{{{x}^{2}}}\]
\[\Rightarrow \sin \theta =\dfrac{\sqrt{1024{{x}^{2}}-{{\left( 512 \right)}^{2}}}}{{{x}^{2}}}.....\left( iv \right)\]
Now, if we take triangle PQR, then its area is given by,
\[\text{Area of }\Delta \text{PQR}=\dfrac{1}{2}\times q\times r\times \sin p\]
Thus, the area of triangle BCD will be given by,
\[\text{Area of }\Delta BCD=\dfrac{1}{2}\times BC\times CD\times \sin \theta \]
\[\Rightarrow \text{Area of }\Delta BCD=\dfrac{1}{2}\times x\times x\times \sin \theta .....\left( v \right)\]
Now, we will substitute the values of the area of triangle BCD and \[\sin \theta \] from (i) and (iv) to (v). Thus, we will get,
\[240=\dfrac{1}{2}\times {{x}^{2}}\times \dfrac{\sqrt{1024{{x}^{2}}-{{\left( 512 \right)}^{2}}}}{{{x}^{2}}}\]
\[\Rightarrow 480=\sqrt{1024{{x}^{2}}-{{\left( 512 \right)}^{2}}}\]
\[\Rightarrow 480=\sqrt{{{2}^{10}}{{x}^{2}}-{{\left( {{2}^{9}} \right)}^{2}}}\left\{ \text{Since }{{2}^{9}}=512;{{2}^{10}}=1024 \right\}\]
\[\Rightarrow 480=\sqrt{{{2}^{10}}{{x}^{2}}-{{2}^{18}}}\left\{ \text{Since }{{\left( {{2}^{x}} \right)}^{y}}={{2}^{x\times y}} \right\}\]
\[\Rightarrow 480=\sqrt{{{2}^{10}}\left( {{x}^{2}}-{{2}^{8}} \right)}\]
\[\Rightarrow 480={{2}^{5}}\sqrt{{{x}^{2}}-{{2}^{8}}}\]
\[\Rightarrow \dfrac{480}{{{2}^{5}}}=\sqrt{{{x}^{2}}-{{2}^{8}}}\]
Now, \[{{2}^{5}}=32,\] so we will get,
\[\Rightarrow \dfrac{480}{32}=\sqrt{{{x}^{2}}-{{2}^{8}}}\]
\[\Rightarrow 15=\sqrt{{{x}^{2}}-{{2}^{8}}}\]
Now, \[{{2}^{8}}=256,\] so we will get,
\[\Rightarrow 15=\sqrt{{{x}^{2}}-256}\]
On squaring both the sides, we will get,
\[{{\left( 15 \right)}^{2}}={{x}^{2}}-256\]
\[\Rightarrow 225+256={{x}^{2}}\]
\[\Rightarrow {{x}^{2}}=481.....\left( vi \right)\]
Now, we know the property of a rhombus that the diagonals bisect each other and are perpendicular to each other. So,
\[BD=2\times OD\]
\[\Rightarrow 32=2\times OD\]
\[\Rightarrow OD=14cm......\left( vii \right)\]
\[AC=2\times OC\]
\[\Rightarrow OC=\dfrac{AC}{2}.....\left( viii \right)\]
Now, we will apply Pythagoras theorem in the right-angled triangle COD. According to this theorem, if H is the hypotenuse, B is the base and P is the perpendicular, then we have,
\[{{H}^{2}}={{P}^{2}}+{{B}^{2}}\]
In our case, H = CD, P = OC and B = OD. Thus, we have,
\[{{\left( CD \right)}^{2}}={{\left( OC \right)}^{2}}+{{\left( OD \right)}^{2}}.....\left( ix \right)\]
From (vii), (viii) and (ix), we have,
\[{{x}^{2}}={{\left( \dfrac{AC}{2} \right)}^{2}}+{{\left( 16 \right)}^{2}}\]
Now, the value of \[{{x}^{2}}\] is 481 (from vi). On substituting this, we get,
\[481={{\left( \dfrac{AC}{2} \right)}^{2}}+256\]
\[\Rightarrow {{\left( \dfrac{AC}{2} \right)}^{2}}=481-256\]
\[\Rightarrow {{\left( \dfrac{AC}{2} \right)}^{2}}=225\]
\[\Rightarrow {{\left( \dfrac{AC}{2} \right)}^{2}}={{\left( 15 \right)}^{2}}\]
\[\Rightarrow \dfrac{AC}{2}=15cm\]
\[\Rightarrow AC=30cm\]
Thus, the length of the other diagonal is 30 cm.

Note: The alternate way of solving the question is shown below. We know that if \[{{d}_{1}}\] and \[{{d}_{2}}\] are the diagonals of a rhombus, then the area of the rhombus is given by the formula,
\[\text{Area of rhombus}=\dfrac{{{d}_{1}}\times {{d}_{2}}}{2}\]
In our case, area of rhombus \[=480c{{m}^{2}},{{d}_{1}}=32cm\] and we have to find \[{{d}_{2}}.\] Thus,
\[480c{{m}^{2}}=\dfrac{32cm\times {{d}_{2}}}{2}\]
\[\Rightarrow {{d}_{2}}\times 16cm=480c{{m}^{2}}\]
\[\Rightarrow {{d}_{2}}=30cm\]