Question

The area of the region bounded by the parabola, ${\left( {y - 2} \right)^2} = x - 1$, the tangent to the parabola at the point (2, 3) and the x-axis is
$\left( a \right)$ 3
$\left( b \right)$ 6
$\left( c \right)$ 9
$\left( d \right)$ 12

Answer 1

Hint: In this particular question use the concept that to find the equation of tangent first find the slope of the tangent by differentiation the equation on which the tangent is drawn and satisfies the points from which the tangent is passing, and use the concept that the equation of line passing through the point $\left( {{x_1},{y_1}} \right)$ having slope m is given as, $\left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$, so use these concepts to reach the solution of the question.

Complete step-by-step answer:

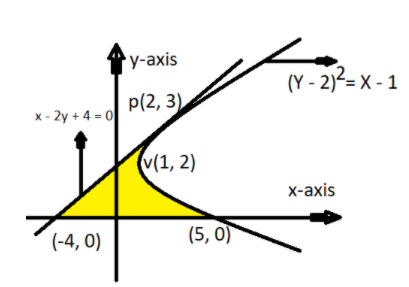
Given equation of parabola
${\left( {y - 2} \right)^2} = x - 1$
As compared with the standard equation of parabola ${Y^2} = 4aX$ the vertex of the given parabola is (1, 2) as shown in the above figure.
Now it is given that there is a tangent to the parabola passing through the point (2, 3).
So first check whether this point is on the parabola or not, if yes then this point satisfies the equation of parabola.
$ \Rightarrow {\left( {3 - 2} \right)^2} = 2 - 1$
$ \Rightarrow 1 = 1$
So the given point is on the parabola.
Now find out the equation of the tangent of the parabola through the point (2, 3).
So differentiate the equation of parabola w.r.t x and satisfies the point (2, 3) we have,
$ \Rightarrow \dfrac{d}{{dx}}{\left( {y - 2} \right)^2} = \dfrac{d}{{dx}}\left( {x - 1} \right)$
$ \Rightarrow 2\left( {y - 2} \right)\dfrac{{dy}}{{dx}} = 1 - 0$
$ \Rightarrow \dfrac{{dy}}{{dx}} = \dfrac{1}{{2\left( {y - 2} \right)}}$
$ \Rightarrow {\left( {\dfrac{{dy}}{{dx}}} \right)_{\left( {2,3} \right)}} = \dfrac{1}{{2\left( {3 - 2} \right)}} = \dfrac{1}{2}$
So the slope of the tangent is, m = $\dfrac{1}{2}$.
Now as we know that the equation of line passing through the point $\left( {{x_1},{y_1}} \right)$ is given as,
$ \Rightarrow \left( {y - {y_1}} \right) = m\left( {x - {x_1}} \right)$
Now the equation of line is passing through, $\left( {{x_1},{y_1}} \right)$ = (2, 3) and slope, m = (1/2) so we have,
$ \Rightarrow \left( {y - 3} \right) = \dfrac{1}{2}\left( {x - 2} \right)$
$ \Rightarrow 2y - 6 = \left( {x - 2} \right)$
$ \Rightarrow x - 2y + 4 = 0$
So this is the equation of the tangent as shown in the above figure.
Now find out the intersection point of this line with the x-axis.
As we know that on x-axis y coordinate is zero, so substitute, y = 0 in the equation of tangent we have,
$ \Rightarrow x - 2\left( 0 \right) + 4 = 0$
$ \Rightarrow x = - 4$
So the intersection point with the x-axis is (-4, 0) as shown in the above figure.
Now we have to find out the area bounded by the parabola, equation of tangent and the x-axis, the required area is shown by yellow color in the graph.
So the area bounded by the curve is given as,
$ \Rightarrow A = \int_{y = {y_1}}^{y = {y_2}} {\left( {{x_1} - {x_2}} \right)dy} $, where ${y_1}{\text{ and }}{y_2}$ are the upper and lower limits and ${x_1}$ is the curve of parabola and ${x_2}$ is equation of tangent.
So, ${y_1} = 0,{y_2} = 3$
And, ${x_1} = {\left( {y - 2} \right)^2} + 1,{x_2} = 2y - 4$
Now substitute the value in the above formula we have,
$ \Rightarrow A = \int_{y = 0}^{y = 3} {\left( {{{\left( {y - 2} \right)}^2} + 1 - \left( {2y - 4} \right)} \right)dy} $
$ \Rightarrow A = \int_{y = 0}^{y = 3} {\left( {{{\left( {y - 2} \right)}^2} - 2y + 5} \right)dy} $
Now as we know that $\int {{{\left( {y - a} \right)}^n}dy} = \dfrac{{{{\left( {y - a} \right)}^{n + 1}}}}{{n + 1}} + C$, where C is some arbitrary integration constant so we have,
$ \Rightarrow A = \left[ {\dfrac{{{{\left( {y - 2} \right)}^3}}}{3} - 2\dfrac{{{y^2}}}{2} + 5y} \right]_0^3$
Now apply the integration limits we have,
$ \Rightarrow A = \left[ {\dfrac{{{{\left( {3 - 2} \right)}^3}}}{3} - 2\dfrac{{{3^2}}}{2} + 5\left( 3 \right) - \left( {\dfrac{{{{\left( {0 - 2} \right)}^3}}}{3} - 0 + 0} \right)} \right]$
Now simplify it we have,
$ \Rightarrow A = \left[ {\dfrac{1}{3} - 9 + 15 + \dfrac{8}{3}} \right]$
$ \Rightarrow A = \left[ {\dfrac{9}{3} - 9 + 15} \right]$
$ \Rightarrow A = \left[ {3 - 9 + 15} \right]$
$ \Rightarrow A = \left[ {18 - 9} \right] = 9$ Sq. units.
So this is the required area bounded by the given curves.
Hence option (c) is the correct answer.

Note: Whenever we face such types of questions the key concept we have to remember is that the area bounded by the curves is given as, $A = \int_{y = {y_1}}^{y = {y_2}} {\left( {{x_1} - {x_2}} \right)dy} $, where ${y_1}{\text{ and }}{y_2}$ are the upper and lower limits and ${x_1}$ is the curve of parabola and ${x_2}$ is equation of tangent, so simply substitute the values and integrate it as above we will get the required answer.