Question

The area of the region bounded by the lines \[y=mx\], \[x=1\], \[x=2\] and \[x-axis\] is 6 sq. units, then 'm' is.
A.. 1
B.. 4
C.. 3
D.. 2

Answer 1

Hint: In these types of questions first of all we need to make the graph of the lines and curves given in the question. Then mark out the region whose area is to be calculated after that find the co-ordinates of points of intersection which are bounding the region of interest. Now we need to apply the formula of calculus to find the area under the curve, the formula is \[Area=\int\limits_{a}^{b}{y\cdot dx}=\int\limits_{a}^{b}{f(x)\cdot dx}\]. In the position of \[f(x)\] we will put the value of \[y\] which is \[y=mx\] given to us in the question. In the place of limits \[a\] and \[b\] we will put the values of \[x\] as \[a=x=1\] and \[b=x=2\] then we will integrate and equate it to 6 sq. units and find the value of m.

Complete step-by-step answer:
Now in this question we need to find the slope of the line which bounds the region of our interest and whose area is known to us.
First of all we will draw the graph by considering all the conditions given in the question and after that we will mark our region of interest and then we will find the co-ordinates of intersection between the lines given to us which bound our region of interest.
Now the graph of the lines given in the question is shown below,

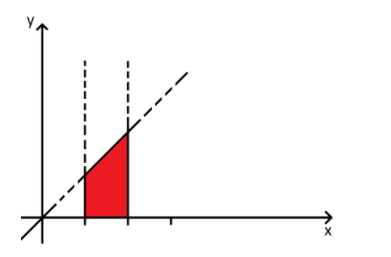
The area of interest is highlighted in the following figure,

We are going to take the help of integral calculus to find the area bounded by these lines, precisely by using Definite integrals,
The formula we are going to use is,
\[Area=\int\limits_{a}^{b}{y\cdot dx}=\int\limits_{a}^{b}{f(x)\cdot dx}\]
The derivation of formula is as follows,
First of all let us take a curve \[y=f(x)\] and let us cut a very thin rectangular strip of height \[y\] and width \[dx\] let there be n number of these strips such that \[dx\to 0\] and \[n\to \infty \]. So now our question has become continuous rather than discrete, so we will use integration to solve this question. The more the number of strips the more accurate our evaluated area will be and hence lesser the errors will be.
Let the area of the rectangular strip be \[dA\] such that \[dA=y\cdot dx\] but we have to find the area under the curve, the whole area between the given limits.

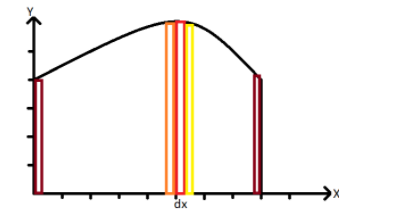
Let us assume the limits for this case are \[x=a\] and \[x=b\],
\[dA=y\cdot dx\]
Integrating both sides, we get,
\[A=\int{y\cdot dx}\]
\[A=\int{f(x)\cdot dx}\]
Now putting the limits in the integral and converting the indefinite integral into definite integral with limits, we get,
\[A=\int\limits_{a}^{b}{f(x)\cdot dx}\]
Now we have derived the formula to find the area under the curve between the given limits.
So now let us proceed with our question,
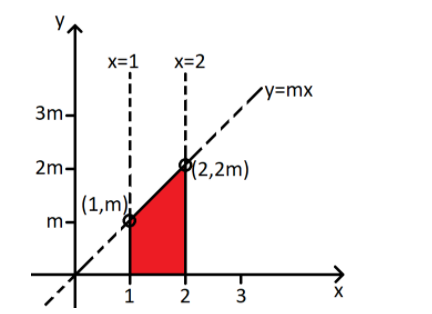
The graph of our region of interest whose area we have to evaluate is given below,

Now as we can see the lines bounding our region of interest in the direction of positive \[x\]-axis, so limits of our integral will be the \[x\] co-ordinates of the lines bounding our region of interest from the extreme beginning of the area of interest to the extreme ending of our area of interest.
We are choosing \[x\] co-ordinates as limits because we have integrated our integral with respect to \[x\] and only the width of our strip is changing to cover all the area because the height is a function and it adjusts itself when we enter the value of \[x\] at any point between the given limits.
So by applying the formula, our integral becomes,
\[A=\int\limits_{a}^{b}{f(x)\cdot dx}\]
Putting the value of function of \[x\]
\[A=\int\limits_{a}^{b}{mx\cdot dx}\]
Putting the value of limits in the integral, we get,
\[A=\int\limits_{1}^{2}{mx\cdot dx}\]
Now we are given with the area of the region of interest, by putting it in the integral we get,
\[6=\int\limits_{1}^{2}{mx\cdot dx}\]
Now integrating the equation, we get,
\[6=m\left| \dfrac{{{x}^{2}}}{2} \right|_{1}^{2}\]
Now the integration rule, subtraction of lower limit from upper limit when put in the integrated function we get,
\[6=m\left( \dfrac{{{2}^{2}}}{2}-\dfrac{{{1}^{2}}}{2} \right)\]
\[6=m\left( \dfrac{4-1}{2} \right)\]
\[6=m\left( \dfrac{3}{2} \right)\]
\[m=4\]
Hence the slope of the line bounding the area from above is 4,
Therefore the correct option is
Option. B. 4

Note: We can use an alternative method to solve this question in which we can instead of integrating with respect to \[x\] we can integrate with respect to \[y\] and we have to choose a rectangular strip such that now the width of the strip will be \[dy\] and its height will be \[x\] or \[f(y)\] and the limits will be for the variable \[y\]. In discrete data solving we use summation whereas in continuous data solving we use integration. The more the number of strips and the thinner they are the more accurate our evaluated area will be because under the curves thick strips will either cut out or include more than needed so we go for thin strips. Sometimes we will be asked to find the area between two curves or functions, in that case consider the rest of the conditions same as stated above in solution, the formula will become,
\[A=\int\limits_{a}^{b}{\left( {{y}_{2}}-{{y}_{1}} \right)\cdot dx}\] or we can write it as \[A=\int\limits_{a}^{b}{\left[ {{f}_{2}}(x)-{{f}_{1}}(x) \right]\cdot dx}\] where \[{{f}_{2}}(x)\] function is above the \[{{f}_{1}}(x)\] function in the graph. Also remember that area is never negative if area is coming negative then take it’s modulus and then add it to the final area. For example definite integral of \[\sin x\] function is \[\int\limits_{0}^{2\pi }{\sin x\cdot dx}=0\] but the area of \[\sin x\] function by keeping the limits same is \[A=\int\limits_{0}^{2\pi }{\sin x\cdot dx}=2\int\limits_{0}^{\pi }{\sin x\cdot dx}\ne 0\].