Question

The area of the region bounded by the curves \[y = \left| {x - 1} \right|\] and $y = 3 - \left| x \right|$ is ?
A.$2$ sq. units
B.$3$ sq. units
C.$4$ sq. units
D.$6$ sq. units

Answer 1

Hint: The given curves are modulus functions. To solve them, we first write them in the form of separated conditional functions. We can then plot their rough graph and find out their points of intersection.

Complete answer: The given curves are $y = \left| {x - 1} \right|$ and $y = 3 - \left| x \right|$
The first curve is $y = \left| {x - 1} \right|$
Thus, $y = x - 1$ for $x \geqslant 1$ … (i)
And $y = - \left( {x - 1} \right)$ for $x < 1$
i.e. $y = 1 - x$ for $x < 1$ … (ii)
Similarly, the second curve is $y = 3 - \left| x \right|$
i.e. $y = 3 - x$ for $x \geqslant 0$ … (iii)
and $y = 3 - \left( { - x} \right)$ for $x < 0$
i.e. $y = 3 + x$ for $x < 0$ … (iv)


We now sketch the graph as follows.
As per the graph, the required area is the area of the quadrilateral ABCD.
This can be calculated by subtracting the area of triangles AED and CDF from the area of the triange EBF.
Thus, required area, $A = $ar(EBF) – ar(AED) – ar(CDF)
Area of a triangle is given by the formula $A = \frac{1}{2} \times b \times h$
Thus, $A = \left( {\frac{1}{2} \times 4 \times 3} \right) - \left[ {\left( {\frac{1}{2} \times 2 \times 2} \right) + \left( {\frac{1}{2} \times 2 \times 1} \right)} \right]$
i.e. $A = 6 - \left( {2 + 1} \right)$
$\therefore A = 3$sq. units

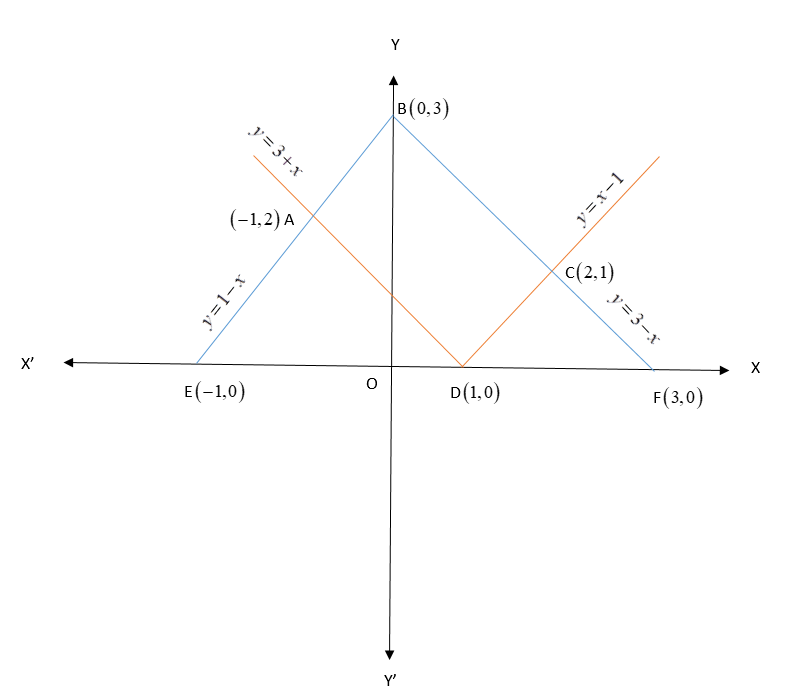
Hence, the area enclosed by the curves $y = \left| {x - 1} \right|$ and $y = 3 - \left| x \right|$ is 3 sq. units.
And hence the correct option is B.

Note:
Such questions involving the use of modulus functions must be solved carefully. It is very important to conditionally separate the given functions first. We also have to remember the formulae for the areas of various different geometrical shapes. Draw a rough graph by plotting all the curves and then calculate the area accordingly.