Question

The area of the pentagon whose vertices are (4,1), (3,6), (-5,1), (-3,-3) and (-3,0) is
A.30 sq. units
B.60 sq. units
C.120 sq. units
D.None of these

Answer 1

Hint: We are given the coordinates of all the five points, we use the formula of area of pentagon which is
Area of the pentagon \[ = \dfrac{1}{2}\left| {\sum {{x_n}{y_{n + 1}} - {y_n}{x_{n + 1}}} } \right|\]; where n = 1, 2, 3, 4, 5. We substitute the values and find the area.

Complete step-by-step answer:
Pentagon is a plane figure with five straight sides and five angles.
Here, the given vertices are (4,1), (3,6), (-5,1), (-3,-3) and (-3,0).

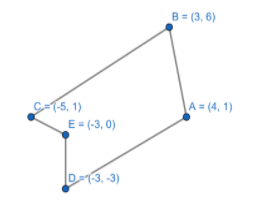
Now, Let,
\[\left( {{x_1},{y_1}} \right)\]=(4,1)
\[\left( {{x_2},{y_2}} \right)\]=(3,6)
\[\left( {{x_3},{y_3}} \right)\]=(-5,1)
\[\left( {{x_4},{y_4}} \right)\]=(-3,-3)
\[\left( {{x_5},{y_5}} \right)\]=(-3,0)
Now, apply the formula of area of a pentagon, which is
\[ = \dfrac{1}{2}\left| {\sum {{x_n}{y_{n + 1}} - {y_n}{x_{n + 1}}} } \right|\]; where n = 1, 2, 3, 4, 5
\[ = \dfrac{1}{2}\left| {\left( {{x_1}{y_2} + {x_2}{y_3} + {x_3}{y_4} + {x_4}{y_5} + {x_5}{y_1}} \right) - \left( {{y_1}{x_2} + {y_2}{x_3} + {y_3}{x_4} + {y_4}{x_5} + {y_5}{x_1}} \right)} \right|\]
Putting the values of xi and yi where i = 1, 2, 3, 4, 5 in the formula we get
\[
  A = \dfrac{1}{2}\left| {\left( {4 \times 6 + 3 \times 1 + \left( { - 5} \right) \times \left( { - 3} \right) + \left( { - 3} \right) \times 0 + \left( { - 3} \right) \times 1} \right) - \left( {1 \times 3 + 6 \times \left( { - 5} \right) + 1 \times \left( { - 3} \right) + \left( { - 3} \right) \times \left( { - 3} \right) + 0 \times 4} \right)} \right|{\text{ }}sq.{\text{ }}units \\
   = \dfrac{1}{2}\left| {\left( {24 + 3 + 15 + 0 - 3} \right) - \left( {3 - 30 - 3 + 9 + 0} \right)} \right|{\text{ }}sq.{\text{ }}units \\
   = \dfrac{1}{2}\left| {39 + 21} \right|{\text{ }}sq.{\text{ }}units \\
   = \dfrac{1}{2}\left| {60} \right|{\text{ }}sq.{\text{ }}units \\
   = 30{\text{ }}sq.{\text{ }}units \\
\]
Hence, the area of the pentagon is 30 sq. units .
Hence, the correct option is (A).

Note: 1. A pentagon is any five –sided polygon. Sometimes it is called 5-gon. The sum of the angles in a simple pentagon is \[540^\circ \].
2.The formula given below is also valid for all polygons ,
\[A = \dfrac{1}{2}\left| {\left( {{x_1}{y_2} + {x_2}{y_3} + {x_3}{y_4} + ..... + {x_{n - 1}}{y_n} + {x_n}{y_1}} \right) - \left( {{y_1}{x_2} + {y_2}{x_3} + {y_3}{x_4} + ..... + {y_{n - 1}}{x_n} + {y_n}{x_1}} \right)} \right|\]