Question

The area of the parallelogram formed by the lines \[y=mx,y=mx+1,y=nx\] and \[y=nx+1\] equals
\[\dfrac{\left| m+n \right|}{\left( m-n \right){}^{2}}\]
\[\dfrac{2}{\left| m+n \right|}\]
\[\dfrac{1}{\left| m+n \right|}\]
\[\dfrac{1}{\left| n-m \right|}\]

Answer 1

Hint: Consider parallelogram as PQRS. Take the 4 lines y = mx and y = mx + 1 are parallel and y = nx and y = nx + 1 are parallel. Parallel lines do not intersect. Thus with 4 lines find the coordinates of their intersection. Then find area by dividing the parallelogram into 2 equal halves i.e. triangles.

Complete step-by-step solution -

We have been given four equations of line,
\[y=mx,y=mx+1,y=nx\] and \[y=nx+1\]
Hence we need to find the area of the parallelogram formed by these lines.
Now the line y = mx and y = mx + 1 are parallel, which means that both these lines won’t intersect. Similarly, the lines y = nx and y = nx +1 are parallel, so they won’t intersect.
Now let us consider each line to get the coordinates of the parallelogram.
\[\begin{align}
  & y=mx-(1) \\
 & y=nx-(2) \\
 & y=mx+1-(3) \\
 & y=nx+1-(4) \\
\end{align}\]
Let us first consider equation (1) and equation (2).
y = mx and y = nx. The intersection point of these two equations passes through the origin. Thus their coordinates are (0, 0). Let us consider this as P (0, 0), which is an intersection point.
Now let us consider (3) and (4). We can equate them as,
\[mx+1=nx+1\]
Cancel out 1 from both sides and simplify it,
\[\begin{align}
  & mx=nx \\
 & mx-nx=0 \\
 & \left( m-n \right)x=0 \\
\end{align}\]
\[\left( m-n \right)\] cannot be zero, as \[m\ne n\].
Thus both lines (3) and (4) are not identical. Hence, put x = 0 in the equation, we get y = 1. Thus we get the second point as Q = (0, 1).
Now let us take equation (1) and equation (4).
\[y=mx\] and \[y=nx+1\], equating them we get,
\[\begin{align}
  & mx=nx+1 \\
 & mx-nx=1 \\
 & \left( m-n \right)x=1 \\
 & \therefore x=\dfrac{1}{m-n} \\
\end{align}\]
Thus put, \[x=\dfrac{1}{m-n}\] in y = mx, we get, \[y=\dfrac{m}{m-n}\].
Thus the coordinates are, \[R=\left( \dfrac{1}{m-n},\dfrac{m}{m-n} \right)\].
Now let us take equation (2) and equation (3).
\[y=nx\] and \[y=mx+1\], let us equate them,
\[\begin{align}
  & nx=mx+1 \\
 & nx-mx=1 \\
 & x\left( n-m \right)=1 \\
\end{align}\]
\[x=\dfrac{1}{n-m}\], put this in y = nx.
We get, \[y=\dfrac{n}{n-m}\]
Thus the coordinates are, \[S=\left( \dfrac{1}{n-m},\dfrac{n}{n-m} \right)\].
Thus we got 4 coordinates of the parallelogram formed by the four lines as,
P = (0, 0), Q = (0, 1), \[R=\left( \dfrac{1}{m-n},\dfrac{m}{m-n} \right)\] and \[S=\left( \dfrac{1}{n-m},\dfrac{n}{n-m} \right)\].
From the figure,

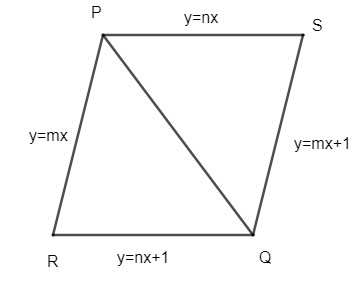
y = nx line is parallelogram to line, y = nx + 1.
Similarly, line y = mx is parallel to y = mx + 1.
Now P is the intersection point of y = mx and y = nx. Similarly, R us the intersection of line y = mx and y = nx + 1.
S is the intersection of y =nx and y = mx + 1. Point Q is the intersection of line y = mx +1 and y = nx + 1.
PQ is the diagonal of the parallelogram. By the properties of the parallelogram, diagonal PQ divides the parallelogram into two equal half i.e. it divides it into 2 equal triangles.
Area of parallelogram = ar \[\left( \Delta PRQ \right)\] + ar \[\left( \Delta PSQ \right)\]
Now ar \[\left( \Delta PRQ \right)\] = ar \[\left( \Delta PSQ \right)\]
\[\therefore \] Area of parallelogram = ar \[\left( \Delta PRQ \right)\] + ar \[\left( \Delta PRQ \right)\]
A = 2 ar \[\left( \Delta PRQ \right)\]
Now let us find the area of \[\left( \Delta PRQ \right)\]
Area of a triangle \[=\dfrac{1}{2}\left| \begin{matrix}
   {{x}_{1}} & {{y}_{1}} & 1 \\
   {{x}_{2}} & {{y}_{2}} & 1 \\
   {{x}_{3}} & {{y}_{3}} & 1 \\
\end{matrix} \right|=\dfrac{1}{2}\left| {{x}_{1}}\left( {{y}_{2}}-{{y}_{3}} \right)-{{x}_{2}}\left( {{y}_{1}}-{{y}_{3}} \right)+{{x}_{3}}\left( {{y}_{1}}-{{y}_{2}} \right) \right|\]
Now we know the coordinates of P, Q and R. Substitute them in the above equation.
\[\begin{align}
  & P=\left( 0,0 \right)=\left( {{x}_{1}},{{y}_{1}} \right) \\
 & Q=\left( 0,1 \right)=\left( {{x}_{2}},{{y}_{2}} \right) \\
 & R=\left( \dfrac{1}{m-n},\dfrac{m}{m-n} \right)=\left( {{x}_{3}},{{y}_{3}} \right) \\
\end{align}\]
\[\therefore \] Area of triangle = \[\dfrac{1}{2}\left| \begin{matrix}
   0 & 0 & 1 \\
   0 & 1 & 1 \\
   \dfrac{1}{m-n} & \dfrac{m}{m-n} & 1 \\
\end{matrix} \right|\]
\[\begin{align}
  & A=\dfrac{1}{2}\left| 0\left[ 1-\dfrac{m}{m-n} \right]-0\left[ 0-\dfrac{1}{m-n} \right]+1\left[ 0-\dfrac{1}{m-n} \right] \right| \\
 & A=\dfrac{1}{2}\left| 0-0+1\times \left( \dfrac{-1}{m-n} \right) \right|=\dfrac{1}{2}\left| \dfrac{-1}{m-n} \right| \\
 & A=\dfrac{1}{2}\left| \dfrac{-1}{-\left( n-m \right)} \right| \\
 & A=\dfrac{1}{2}\left| \dfrac{1}{n-m} \right| \\
\end{align}\]
We got area of triangle PQR \[=\dfrac{1}{2}\left| \dfrac{1}{n-m} \right|=ar\left( \Delta PRQ \right)\]
\[\therefore \] Area of parallelogram \[=2\times ar\left( \Delta PRQ \right)\]
                                              \[=2\times \dfrac{1}{2}\left| \dfrac{1}{n-m} \right|=\left| \dfrac{1}{n-m} \right|\]
\[\therefore \] Hence area of parallelogram = \[\left| \dfrac{1}{n-m} \right|\]
\[\therefore \] Option (d) is the correct answer.

Note: You should understand how to take the coordinates of the parallelogram from the given equation of 4 lines. In parallelograms opposite sides are parallel. So use this property to classify them and accordingly find the lines that intersect points P, Q, R, S.