Question

The area of the minor segment of the circle of radius $ 14\;cm $ , when the angles of the corresponding sector is $ 60^\circ $ , is
A) $ \dfrac{{308}}{3} - 98\sqrt 3 \;c{m^2} $
B) $ \dfrac{{308}}{3} + 49\sqrt 3 \;c{m^2} $
C) $ \dfrac{{308}}{3} + 98\sqrt 3 \;c{m^2} $
D) $ \dfrac{{308}}{3} - 49\sqrt 3 \;c{m^2} $

Answer 1

Hint: In this question, we need to find the area of the corresponding minor segment. Here, we will find the angles of the triangle using the properties of the triangle and determine the type of triangle i.e., equilateral, isosceles or scalene. Then apply the values in the area of the triangle. Next, we will find the area of the sector using the formula of the area of sector. Finally, substitute the values of area of triangle and the area of sector in the formula of area of minor segment and evaluate it to determine the solution.

Complete step-by-step answer:
It is given that the central angle $ \angle AOB $ of a sector i.e., $ \theta = 60^\circ $
And the radius of the circle, $ r = 14\;cm $
Here, we need to find the area of the corresponding minor segment.
Let the center of the circle be $ O $ .
Let the radii of the sector be $ OA $ and $ OB $ .

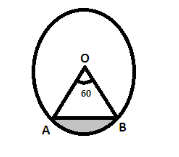
In $ \Delta AOB $ we have, $ OA = OB $
Therefore, $ \angle OAB = \angle OBA $ (In a triangle, equal sides have equal angles opposite to them)
  $ \Rightarrow \angle OAB + \angle OBA = 2\angle OBA $ (Or)
  $ \Rightarrow \angle OAB + \angle OBA = 2\angle OAB $
Now, we have, $ \theta = 60^\circ $
Now, $ \angle OAB + \angle OBA + \angle AOB = 180^\circ $ (The angle sum property of the triangles)
 $ \Rightarrow 2\angle OAB + 60^\circ = 180^\circ $
Therefore, $ 2\angle OAB = 180^\circ - 60^\circ $
 $ \Rightarrow 2\angle OAB = 120^\circ $
 $ \Rightarrow \angle OAB = 60^\circ = \angle OBA $
Thus, $ \Delta AOB $ is equilateral triangle with side $ a = 14\;cm $
Therefore, area of the triangle $ \Delta AOB $ = $ \dfrac{{\sqrt 3 }}{4} \times {a^2} $
 $ = \dfrac{{\sqrt 3 }}{4} \times 14 \times 14\;c{m^2} $
= $ 49\sqrt 3 \;c{m^2} $
Also, the area of the sector $ AOB $ = $ \pi {r^2}\dfrac{\theta }{{360^\circ }} $ , when $ \theta $ is the central angle and $ r $ = radius of the sector
 $ = \dfrac{{22}}{7} \times 14 \times 14 \times \dfrac{{60}}{{360}}\;c{m^2} $
 $ = \dfrac{{308}}{3}\;c{m^2} $
Now, area of minor segment = $ \pi {r^2}\dfrac{\theta }{{360^\circ }} - \dfrac{1}{2}{r^2}\sin \theta $
 $ = \dfrac{{308}}{3} - 49\sqrt 3 \;c{m^2} $
Hence, option D) $ \dfrac{{308}}{3} - 49\sqrt 3 \;c{m^2} $ is the correct answer.
So, the correct answer is “Option D”.

Note: It is worthy to note here that, the angle sum property of the triangle states that the sum of interior angles of a triangle is $ 180^\circ $ . However, we can also determine the area of the major sector by the formula area of the major segment= $ \pi {r^2} - $ area of the minor segment.