Question

The area of the house made of glass with dimensions $30 \times 25 \times 25c{m^3}$ in (sq. cm) is
a. 3120
b. 4250
c. 5380
d. 6880

Answer 1

Hint: The house will have the shape of a cuboid. We are given the length, breadth and height of the house, which is a cuboid. We will calculate the surface area of the cuboid using the formula, \[2\left[ {lb + bh + hl} \right]\], where $l$ represents the length, $b$ represents the breadth and $h$ represents the height of the cuboid.

Complete step-by-step answer:
From the given question, we have the length of the house as 30 cm, breadth of the house as 25 cm and height of the house is 25 cm.

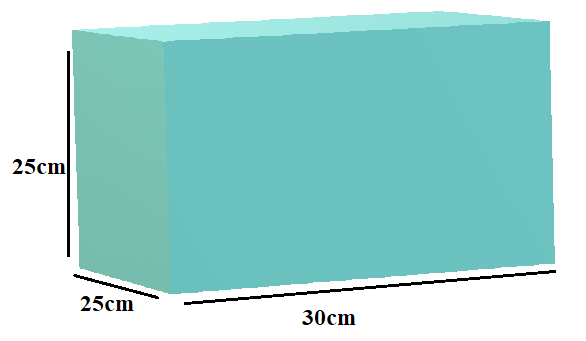
We have to find the area of the house.
We know that there are 6 faces of the cuboid.
The area of all the 6 faces of the cuboid is \[2\left[ {lb + bh + hl} \right]\], where $l$ represents the length, $b$ represents the breadth and $h$ represents the height of the cuboid.
On substituting the values of $l$,$b$ and $h$ in the formula of total surface area of the house is
$
  2\left( {30 \times 25 + 25 \times 25 + 25 \times 30} \right)c{m^2} \\
   \Rightarrow 2\left( {750 + 625 + 750} \right)c{m^2} \\
   \Rightarrow 2\left( {2125} \right)c{m^2} \\
   \Rightarrow 4250c{m^2} \\
$
Hence, the area of the house is 4250 $c{m^2}$
Thus, option b is correct.

Note: Total surface area is the area of all the faces of the cuboid whereas the curved surface area of the cuboid is the area of only 4 faces of the cuboid. Since, we have to find the area of the house, we will find the area of all six faces of the house.