Question

The area of the hall is $288{{m}^{2}}$. If the length was increased by 6m and the breadth decreased by 4m, the area would be unaltered, find the length of the room.

Answer 1

Hint: First, we know that the area A of the rectangle with length l and breadth b is given by$A=l\times b$. Then, by substituting the value of A given in the question as 288, we get the value of b in terms of l. Then, we are given the question with the condition that length is increased by 6 m and breadth is decreased by 4m. Still the area is the same and by substituting the value of b in the expression of the new area, we get the value of length.

Complete answer:
In this question, we are supposed to find the length of the room when the area of the room is $288{{m}^{2}}$ and its length was increased by 6m and the breadth decreased by 4m, the area would be unaltered.
So, before proceeding for this, we must know that the room is of the shape of the rectangle whose area is given as 288 and let us assume its length be l and breadth be b, so the diagram for room look as:

So, we know that the area A of the rectangle with length l and breadth b is given by:
$A=l\times b$
Now, by substituting the value of A given in the question as 288, we get the value of b in terms of l as:
$\begin{align}
  & 288=l\times b \\
 & \Rightarrow b=\dfrac{288}{l} \\
\end{align}$
Now, we are given in the question with the condition that length is increased by 6 m and breadth is decreased by 4m still the area is same can be drawn as:

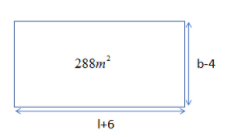
So, by using the same formula for the area of new rectangle as:
$\left( l+6 \right)\left( b-4 \right)=288$
Now, by substituting the value of b calculated above in the above expression, we get:
$\left( l+6 \right)\left( \dfrac{288}{l}-4 \right)=288$
Now, by solving the above expression, we get the value of l as:
$\begin{align}
  & \left( l+6 \right)\left( \dfrac{72}{l}-1 \right)=72 \\
 & \Rightarrow \left( l+6 \right)\left( 72-l \right)=72l \\
 & \Rightarrow 72l+432-6l-{{l}^{2}}=72l \\
 & \Rightarrow {{l}^{2}}+6l-432=0 \\
\end{align}$
Now, by using the quadratic formula for the equation of form $a{{x}^{2}}+bx+c=0$ is given by:
$x=\dfrac{-b\pm \sqrt{{{b}^{2}}-4ac}}{2a}$
Then, by using the above quadratic equation for length in the above formula to get the value of l as:
$\begin{align}
  & l=\dfrac{-6\pm \sqrt{{{6}^{2}}-4\left( 1 \right)\left( -432 \right)}}{2\left( 1 \right)} \\
 & \Rightarrow l=\dfrac{-6\pm \sqrt{36+1728}}{2} \\
 & \Rightarrow l=\dfrac{-6\pm \sqrt{1764}}{2} \\
 & \Rightarrow l=\dfrac{-6\pm 42}{2} \\
\end{align}$
So, we get two values of l by the conditions as:
$\begin{align}
  & l=\dfrac{-6+42}{2} \\
 & \Rightarrow l=\dfrac{36}{2} \\
 & \Rightarrow l=18 \\
\end{align}$ and $\begin{align}
  & l=\dfrac{-6-42}{2} \\
 & \Rightarrow l=\dfrac{-48}{2} \\
 & \Rightarrow l=-24 \\
\end{align}$
So, we know that l is the length of the rectangle which can’t be negative.
Hence, the length of the given room is 18 m.

Note:
Now, to solve these types of questions we need to know another method of solving the quadratic equation which is factorization method as we can factorize the middle term in two components so that after taking common terms, we get the values of x.