Question

What will be the area of the field ABGFEA?

(a) 7225 \[{{m}^{2}}\]
(b) 8225 \[{{m}^{2}}\]
(c) 6225 \[{{m}^{2}}\]
(d) 6725 \[{{m}^{2}}\]

Answer 1

Hint: From the figure consider the 4 triangles and trapezium for which base and height values are given. Find the area of the individual fields and add them together to find the area of field ABGFEA. We will make use of the formulas,
Area of triangle = \[\dfrac{1}{2}\times \] base \[\times \] height
Area of trapezium = \[\dfrac{1}{2}\times \] (sum of parallel sides) \[\times \] height

Complete step by step answer:
Given to us a field ABGFEA for which we need to find the area. The field is divided into 4 triangles and one trapezium, if you look at the figure. Thus we can say that the area of field is given as,
Area of ABGFEA = Area of \[\Delta ABC\] + Area of trapezium BCHG + Area of \[\Delta GHF\] + Area of \[\Delta FDE\] + Area of \[\Delta ADE\] - (1)
Before we move on, let us learn the formula to calculate the area of triangle and trapezium.
We have been given the base and height for calculating the area of triangle. Thus, we can say that,

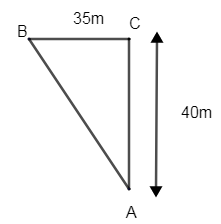
Area of triangle = \[\dfrac{1}{2}\times \] base \[\times \] height
\[\therefore \] Area of triangle = \[\dfrac{1}{2}bh\]
For finding the area of trapezium we require the length of opposite side and height.

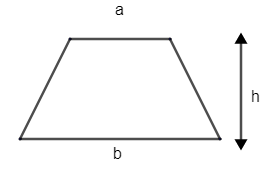
Area of trapezium = \[\left( \dfrac{a+b}{2} \right)h\]
Now let us find the area of each smaller field in ABGFEA.
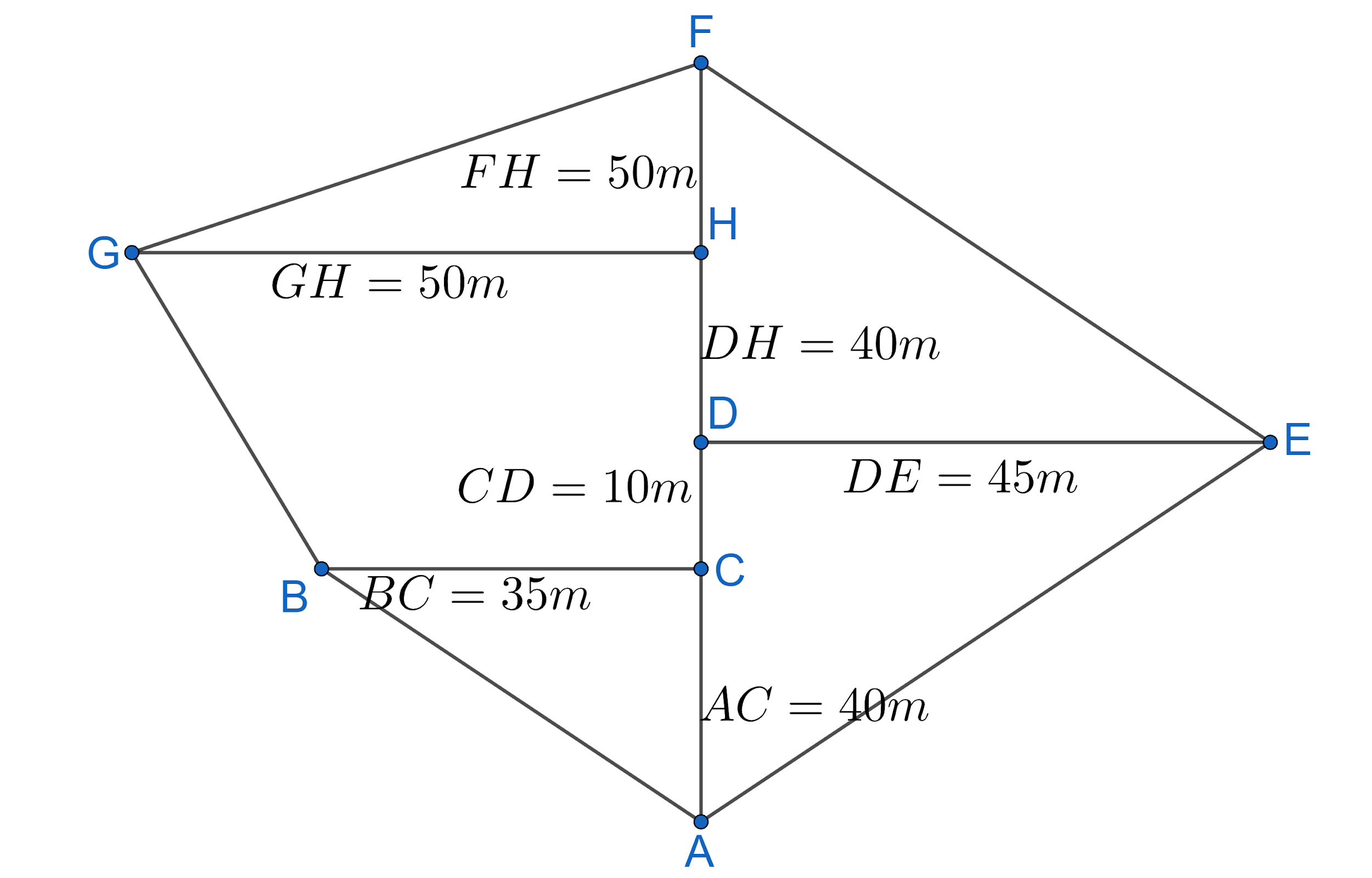
First let us find area of \[\Delta ABC\]. We have been given,
Base = b = 35m, height = h = 40m.
\[\therefore \] Area of \[\Delta ABC=\dfrac{1}{2}bh=\dfrac{1}{2}\times 35\times 40\]
Area of \[\Delta ABC\] = \[35\times 20=700{{m}^{2}}\]
\[\therefore ar\left( \Delta ABC \right)=700{{m}^{2}}\] - (2)
Now let us find area of trapezium BGHC

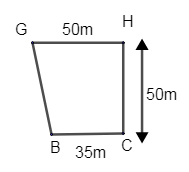
From the figure, HC = HD + DC = 40 + 10 = 50 m
Height of trapezium = h = 50m.
a = 50m and b = 35m
\[\therefore \] Area of trapezium = \[\left( \dfrac{50+35}{2} \right)\times 50=85\times 25=2125{{m}^{2}}\]
\[\therefore ar\left( BGHC \right)=2125{{m}^{2}}\] - (3)
Area of \[\Delta GHF\], where b = 50m and h = 50m.

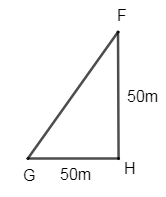
Area of \[\Delta GHF\] = \[\dfrac{1}{2}bh=\dfrac{1}{2}\times 50\times 50=1250{{m}^{2}}\]
\[\therefore \] \[ar\left( \Delta GHF \right)=1250{{m}^{2}}\] - (4)
Area of \[\Delta FDE\], where b = 45m.
Height, h = FD = FH + HD = 50 + 40 = 90m.
Height of triangle FDE = h = 90m.

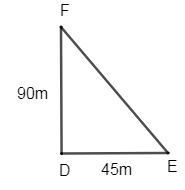
\[\therefore \] Area of \[\Delta FDE=\dfrac{1}{2}bh=\dfrac{1}{2}\times 45\times 90=2025{{m}^{2}}\]
\[ar\left( \Delta FDE \right)=2025{{m}^{2}}\] - (5)
Now area of \[\Delta DAE\], where base = 45cm.
Height of \[\Delta DAE=DA+DC+CA=10+40=50\]m

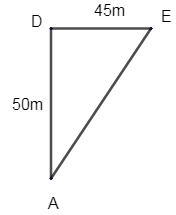
\[\therefore \] Height of \[\Delta DAE\] = 50m = h.
\[\therefore \] Area of \[\Delta DAE\] = \[\dfrac{1}{2}bh=\dfrac{1}{2}\times 50\times 45=1125{{m}^{2}}\] - (6)
Now we have found out the area of the smaller fields. Now substitute all these values in equation (1).
\[\therefore \] Area of the field ABGFEA = ar (ABC) + ar (BGHC) + ar (GHF) + ar (FDE) + ar (DAE)
\[\therefore \] Area of the field ABGFEA = 700 + 2125 + 1250 + 2025 + 1125 = 7225\[{{m}^{2}}\].
Hence the total area of the given field ABGFEA is 7225 \[{{m}^{2}}\].

So, the correct answer is “Option A”.

Note: The question is direct application of the area of triangle and trapezium. Be careful while finding the height of different triangular sections from the figure. And remember the formula to find the area for the same. Here we were given the height of the trapezium directly as the side was a vertical line. But, in case it was not vertical and inclined, we could have found it by dropping a perpendicular from one vertex to the opposite parallel side and then applying the Pythagoras theorem in the triangle so formed.