Question

The area of the circle inscribed in a square of side a, is \[{a^2}c{m^2}\] . With justification, state whether the statement is:
 (A): True, since the radius of the circle is \[\dfrac{a}{2}\] .
(B): False, since the radius of the circle is \[\dfrac{a}{2}\] .
(C): True, since the radius of the circle is \[\dfrac{a}{4}\] .
(D): False, since the radius of the circle is \[\dfrac{a}{4}\] .

Answer 1

Hint: The circle is given to be inscribed in a square whose area is already given to be a² cm² and each side of the square is given to be a cm. We need to justify whether the given statement is true or false, explaining the reasons.
So, by using the formula for the area of the circle i.e:
Area of circle = $\Pi\times{r^2}$
We can find the radius of the circle with the help of the given side of the square in which the given circle is being inscribed. As the circle is properly inside the square touching its sides, the diameter of the circle would be equal to the side of the square.

Complete step-by-step answer:
Step1: The side of the square is given to be ‘ \[a\] ’ cm.

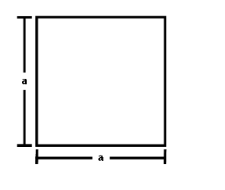
Step2: The circle has been inscribed in the square that means the side of the square is equal to the diameter of the circle:

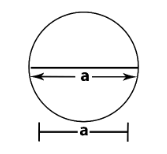
Therefore, the diameter of the circle = \[a{\text{ }}cm\]
because the side of the square is given to be \[a{\text{ }}cm\] .
Step3: The radius of the circle is half of its diameter.
 Hence, Radius of circle = \[\dfrac{1}{2} \times {\text{ }}diameter{\text{ }}of{\text{ }}the{\text{ }}circle\]
i.e Radius \[ = \;\dfrac{1}{2}{\text{ }} \times a\]
i.e Radius = \[\dfrac{a}{2}\;cm\]
Hence, the radius of the circle comes out to be \[\dfrac{a}{2}\;cm\] .
Step4: Now, applying the formula of the area of circle,
 Area = \[{a^2}\;c{m^2}\]
r =\[\dfrac{a}{2}\;cm\]
  \[ = \pi {\text{ }} \times {\text{ }}\left( {\dfrac{{{a^2}}}{4}} \right)\]
= \[\dfrac{\pi }{4}{a^2}\;c{m^2}\]
Hence, the given statement i.e the area of the circle is false.
So, option ‘B’ is correct.
So, the correct answer is “Option b”.

Note: When the circle has been inscribed in a square, that means the circle is fixed in the square and the circle is touching the sides of the square at their midpoints.
Hence, the diameter of the circle becomes equal to the side of the square.
Now, in option ;A’, the radius is given to be \[\dfrac{a}{2}\;cm\] , which is correct by its also mentioned that because the radius of circle is \[\dfrac{a}{2}\;cm\] , the above statement is true which is inappropriate.
In option ‘C’, the radius of the circle is given to be \[\dfrac{a}{4}\;cm\] which is incorrect itself and similar is the case with option ‘D’.
In the option ‘B’, it is properly mentioned that the given statement is false because the radius of the circle comes out to be \[\dfrac{a}{2}\;cm\] which is exactly appropriate. Hence, option ‘B’ is correct.