Question

The area of rhombus is 240 ${cm}^{2}$ and one of the diagonals is 16cm. Find another diagonal.

Answer 1

Hint: We will use the direct formula of the area of the rhombus as it involves length of both the diagonals.

Complete step-by-step answer:
First, let us see the figure of the question.

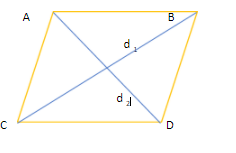
This is the rhombus of area 240 ${cm}^{2}$.
Let its sides be A, B, C and D.
Let us denote one of its diagonals as $d_1$ and the other as $d_2$.
It is given that one of its diagonals $d_1$ is 16cm.
Let the other diagonal $d_2$ be x cm.
We know that the formula of area of the rhombus is: $area = \dfrac{1}{2} \times {d_1} \times {d_2}$
Therefore, the area of the rhombus ABCD = $\dfrac{1}{2} \times 16 \times x$
$
   \Rightarrow 240 = \dfrac{1}{2} \times 16 \times x \\
   \Rightarrow x = 240 \times 2 \times \dfrac{1}{{16}} \\
   \Rightarrow x = \dfrac{{240}}{8} \\
   \Rightarrow x = 30cm \\
 $

Hence, the other diagonal of the given rhombus is found to be 30 cm.

Note: : The diagonals of the rhombus intersect each other and cut each other in equal parts. So, if any side of the rhombus has been given, then we can also find the area of the rhombus without applying the formula of area of the rhombus.