Question

The area of rectangular carpet is \[120{m^2}\] and its perimeter is 46m. The length of its diagonal is
A) 15 m
B) 16 m
C) 17 m
D) 20 m

Answer 1

Hint: Here, we apply the formula for the area as well as the perimeter of a rectangle to find the length and breadth of the rectangle and then we will apply the Pythagoras theorem to find the length of the diagonal of the rectangle.
The area of the rectangle is given by:-
\[area = length \times breadth\]
The perimeter of the rectangle is given by:
\[perimeter = 2(length + breadth)\]

The Pythagoras theorem states that the sum of squares of the base and height of a triangle is equal to the square of its hypotenuse.
\[{\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {height} \right)^2}\]

Complete step by step solution:
It is given that area of the rectangle is \[120{m^2}\]
The perimeter of the rectangle is $46m$.

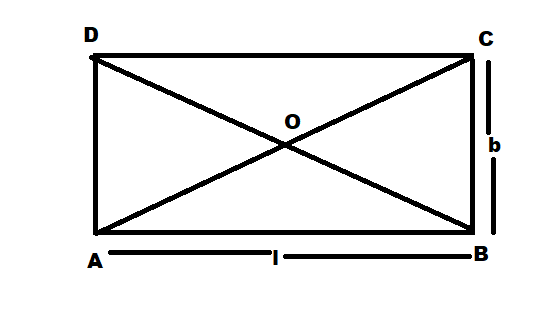
Let ABCD be the rectangle with length=\[l\] and breadth= \[b\]
Then, the area of the rectangle is given by:-
\[area = length \times breadth\]
Therefore putting in the values we get:-
 \[120 = l \times b.....................\left( 1 \right)\]
Also, the perimeter of the rectangle is given by:
\[perimeter = 2(length + breadth)\]
Putting in the values we get:-
\[ 46 = 2\left( {l + b} \right) \]
$ l + b = \dfrac{{46}}{2} $
On simplification,
$ l + b = 23.............\left( 2 \right) $
Now solving equations 1 and 2 we get:-
From equation 2 we get:-
\[b = 23 - l.....................\left( 3 \right)\]
Putting this value in equation 1 we get:-
\[
  l\left( {23 - l} \right) = 120 \\
  23l - {l^2} = 120 \\
  {l^2} - 23l + 120 = 0 \\
 \]
Solving this quadratic equation by middle term split we get:-
\[ {l^2} - 15l - 8l + 120 = 0 \]
\[ l\left( {l - 15} \right) - 8\left( {l - 15} \right) = 0 \]
on simplification,
\[ \left( {l - 15} \right)\left( {l - 8} \right) = 0 \]
\[ l = 15;\, l = 8 \]
Putting the value of $l$ back in equation 3 we get:-
When $l=15m$
Then,
\[b = 23 - 15 \]
$\Rightarrow b = 8 $

When $l=8m$
\[\Rightarrow b = 23 - 8 \]
$\Rightarrow b = 15$
Now applying Pythagoras theorem in \[\Delta ABC\] we get:-
Since the formula of Pythagoras is given by:-
\[{\left( {hypotenuse} \right)^2} = {\left( {base} \right)^2} + {\left( {height} \right)^2}\]
Therefore,
\[{\left( {AC} \right)^2} = {\left( {AB} \right)^2} + {\left( {BC} \right)^2}\]
Which implies:
\[{\left( {diagonal} \right)^2} = {\left( {length} \right)^2} + {\left( {breadth} \right)^2}\]
Now putting in the values we get:-
\[\Rightarrow {\left( {diagonal} \right)^2} = {\left( 8 \right)^2} + {\left( {15} \right)^2} \]
 $\Rightarrow {\left( {diagonal} \right)^2} = 64 + 225$
$\Rightarrow {\left( {diagonal} \right)^2} = 289 $
$\Rightarrow diagonal = \sqrt {289} $
$\Rightarrow diagonal = 17m $

$\therefore$ The length of the diagonal is 17 meter. Hence, option (C) is the correct answer.

Note:
The student can also apply quadratic formula to solve the quadratic equation and find the value of \[l\]
For any quadratic equation of the form \[a{x^2} + bx + c = 0\]
The roots of the equation are given by:-
\[x = \dfrac{{ - b \pm \sqrt {{b^2} - 4ac} }}{{2a}}\]
Hence applying this formula for the equation
 \[{l^2} - 23l + 120 = 0\]
We get:-
\[
  l = \dfrac{{ - \left( { - 23} \right) \pm \sqrt {{{\left( { - 23} \right)}^2} - 4\left( 1 \right)\left( {120} \right)} }}{{2\left( 1 \right)}} \\
  l = \dfrac{{23 \pm \sqrt {529 - 480} }}{2} \\
  l = \dfrac{{23 \pm \sqrt {49} }}{2} \\
  l = \dfrac{{23 \pm 7}}{2} \\
  l = \dfrac{{23 + 7}}{2}or{\text{ }}l = \dfrac{{23 - 7}}{2} \\
  l = \dfrac{{30}}{2}or{\text{ }}l = \dfrac{{16}}{2} \\
  l = 15cm{\text{ }}or{\text{ }}l = 8cm \\
 \].