Question

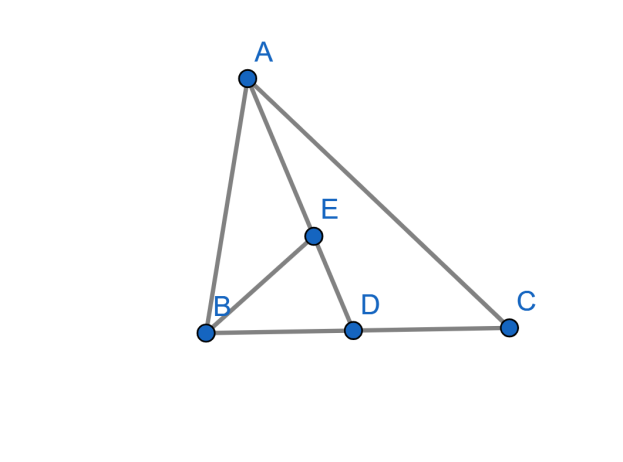
The area of \[\Delta ABC\] is \[32\] square cm. AD is median and E is the midpoint of AD. Find the area of \[\Delta BED\].

Answer 1

Hint: From the given question we have been asked to find the area of the triangle \[\Delta BED\] where the area of triangle \[\Delta ABC\] is given. For solving this question we have to take the median in the triangle \[\Delta ABC\] using that we will use the property in similar triangles that is we bring the relation among the areas of the triangles inscribed in it and further solve the given question using basic mathematical operation like multiplication etc…so, the solution will be as follows.

Complete step by step solution:
Firstly, from the figure which is given we know that in \[\Delta ADB\] BE is the median line.
Which means the area of the triangle, \[\Delta ADB\] is equally separated or we can say that the median divides the given figure in equal parts.
So, we can say that,
\[\Rightarrow area(\Delta BED)=area(\Delta AEB)\]
From the question we are given that AD is the median of the triangle \[\Delta ABC\]. So, we can say that the area is equally divided or simply the area of the triangle \[\Delta ADB\] and \[\Delta ADC\]are equal.
So, we get,
\[\Rightarrow area(\Delta BED)=area(\Delta AEB)=\dfrac{1}{2}area(\Delta ABD)\]
So, we substitute the given area of \[\Delta ABC\] as \[32\] square cm.
We get the equation reduced as follows.
\[\Rightarrow area(\Delta BED)=\dfrac{1}{2}(16)sqcm\]
\[\Rightarrow area(\Delta BED)=8sqcm\]

Note: Students must be very careful in doing the calculations. Students should know the concept of triangles and median to triangle concepts.
For solving this question we use similar triangles concepts. We should know that \[ area(\Delta BED)=area(\Delta AEB)=\dfrac{1}{2}area(\Delta ABD)\] to solve the question.