Question

The area of a square field is $24,200{{m}^{2}}$ . How long will Maya take to cross the field diagonally at the rate of $6.6km/hr$ ?

Answer 1

Hint: Here in this question we have been asked to find the time that Maya takes to cross the square field diagonally which has $24,200{{m}^{2}}$ at the rate of $6.6km/hr$ . We know that the area of the square is equal to the length of the side raised to the power two. Speed is equal to the distance travelled by the time taken.

Complete step by step answer:
Now considering from the question we have been asked to find the time that Maya takes to cross the square field diagonally which has $24,200{{m}^{2}}$ at the rate of $6.6km/hr$ .
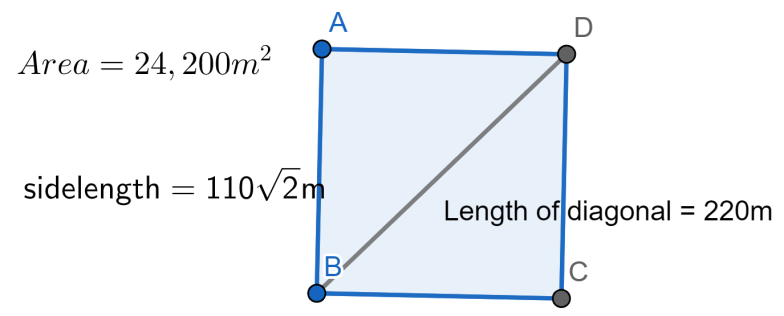
From the basic concepts we know that the area of the square is equal to the length of side raised to the power two that can be mathematically given as $Area={{\left( side \right)}^{2}}$ .
Hence we can say that the length of the side of the given square field will be given as
 $\begin{align}
  & \Rightarrow \sqrt{24,200}m \\
 & \Rightarrow 110\sqrt{2}m \\
\end{align}$ .
From the Pythagoras theorem we can say that the square of the length of the diagonal in a square will be equal the sum of the square of the two times of the side length since a right angle triangle is formed inside a square and diagonal is hypotenuse of it.
Hence we can say that the length of the diagonal of a square will be equal to
$\begin{align}
  & \Rightarrow \sqrt{2\times {{\left( 110\sqrt{2} \right)}^{2}}} \\
 & \Rightarrow 110\sqrt{2}\left( \sqrt{2} \right) \\
 & \Rightarrow 220m \\
\end{align}$.

Speed is equal to the distance travelled by the time taken that can be mathematically given as $Speed=\dfrac{\text{distance travelled}}{time}$ .
As given that the speed of Maya is $6.6km/hr$ that is
$\begin{align}
  & \Rightarrow 6.6\times \dfrac{1000}{60\times 60}\dfrac{m}{\sec } \\
 & \Rightarrow 6.6\times \left( \dfrac{5}{18} \right)\dfrac{m}{\sec } \\
\end{align}$
Now by using the speed formula we can say that $6.6\left( \dfrac{5}{18} \right)=\dfrac{220}{time}$ .
By further simplifying this we will have
$\begin{align}
  & time=\dfrac{220}{6.6\left( \dfrac{5}{18} \right)} \\
 & \Rightarrow \dfrac{220\times 18\times 10}{66\times 5}=\dfrac{2\times 10\times 18\times 2}{6} \\
 & \Rightarrow 2\times 3\times 10\times 2=120\min \\
\end{align}$

Therefore we can conclude that the time taken by Maya to cross the square field diagonally which has $24,200{{m}^{2}}$ at the rate of $6.6km/hr$ is given as $120\sec =2\min $

Note: While answering this type of questions we have to be sure with the calculations that we are going to perform and the concepts that we are going to apply in between the steps in order to answer them. This is a very simple and easy question and can be answered accurately within a short span of time. Very few mistakes are possible in this type of question. If someone had a made a mistake while converting the speed from one units to other units then we will end up having a wrong answer for example if we consider
 $\begin{align}
  & \Rightarrow 6.6\times \dfrac{1000}{60}\dfrac{m}{\sec } \\
 & \Rightarrow 6.6\times \left( \dfrac{50}{3} \right)\dfrac{m}{\sec } \\
\end{align}$
then we will have the answer as
$\begin{align}
  & time=\dfrac{220}{6.6\left( \dfrac{50}{3} \right)} \\
 & \Rightarrow \dfrac{220\times 3\times 10}{66\times 50}=\dfrac{2\times 3\times 2}{6} \\
 & \Rightarrow 2\sec \\
\end{align}$