Question

The area of a right-angle triangle is \[20c{m^2}\] and one of the sides containing the right angle is 4cm. then altitude on hypotenuse is
A.8cm
B.10cm
C.\[\dfrac{{10}}{{\sqrt {41} }}cm\]
D.\[\dfrac{{20}}{{\sqrt {29} }}cm\]

Answer 1

Hint: We are given with the right angled triangle. One of the sides is given to us as 4cm. but that is not the hypotenuse because it is the side that contains the right angle. We will form a diagram. We need to find the hypotenuse so that we can take it as base and then find the altitude.
Using the formula of area of the triangle we will find the height of the triangle. Now since we have both the sides we will find the hypotenuse. Now we have hypotenuse as the base and the area is already given. So again using the same formula we will find the altitude on hypotenuse.
Formula used:
\[area = \dfrac{1}{2} \times b \times h\]

Complete step by step solution:
We will first draw a right-angled triangle with base equals to 4cm.

Now to find the height,
\[area = \dfrac{1}{2} \times b \times h\]
Putting the values,
\[20 = \dfrac{1}{2} \times 4 \times h\]
To find the value of h we will cross multiply,
\[h = \dfrac{{20 \times 2}}{4}\]
On dividing we get,
\[h = 10cm\]
This is the height. Now using the theorem of Pythagoras we will find the value of hypotenuse.
\[hypt = \sqrt {{h^2} + {b^2}} \]
Putting the values,
\[hypt = \sqrt {{{10}^2} + {4^2}} \]
Taking the squares,
\[hypt = \sqrt {100 + 16} \]
On adding we get,
\[hypt = \sqrt {116} \]
Now we will write 116 as a product of 4 and 29.
\[hypt = \sqrt {4 \times 29} \]
4 is the perfect square of 2.
\[hypt = 2\sqrt {29} cm\]

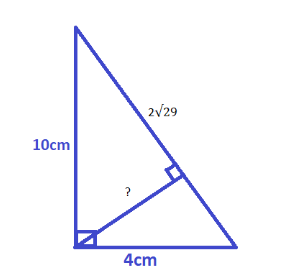
now we have the same triangle but the base and height is changed now. Still we will use the same formula to find the altitude. So now again using the formula,
\[area = \dfrac{1}{2} \times b \times h\]
Putting the values,
\[20 = \dfrac{1}{2} \times 2\sqrt {29} \times h\]
To find the height or altitude here, cross multiplying
\[h = \dfrac{{20 \times 2}}{{2\sqrt {29} }}\]
Cancelling 2 we can write,
\[h = \dfrac{{20}}{{\sqrt {29} }}cm\]
This is the measurement of the altitude. \[h = \dfrac{{20}}{{\sqrt {29} }}cm\]
So, the correct answer is “ \[h = \dfrac{{20}}{{\sqrt {29} }}cm\]”.

Note: Here students might get confused in two things in this question. On is the side that contains the right angle and the other is altitude on hypotenuse. So be clear that the side that contains the right angle can be base or height but never the hypotenuse as exact. And for the second altitude on the hypotenuse is from the vertex point that is the right angle. So don’t get confused!