Question

The area of a rhombus is 2016 squares centimetres, and its side is 65 cm. The lengths of the diagonals (in cm) respectively are:
A) 125,35
B) 126,32
C) 132,26
D) 135,25

Answer 1

Hint:
In this question, we need to determine the lengths of the diagonals of the rhombus whose area is 2016 squares centimetres and its side is 65 cm. For this, we will explore the properties of the rhombus which is given as ${A_r} = \dfrac{1}{2} \times {d_1} \times {d_2}$ and diagonals bisects at 90 degrees.

Complete step by step solution:
Let us consider a rhombus ABCD of side 65 cm with the diagonals ${d_1}$ and ${d_2}$.

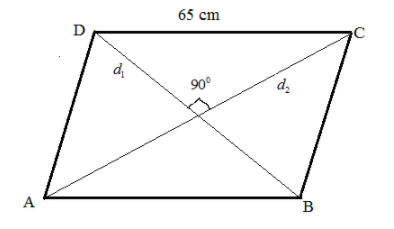
According to the question, the area of the rhombus is given as 2016 squares centimetres.
Also, we know that half of the product of the lengths of the diagonals results in the area of the rhombus. Mathematically, ${A_r} = \dfrac{1}{2} \times {d_1} \times {d_2}$.
Here, substitute the area of the rhombus as 2016 squares centimetres in the formula ${A_r} = \dfrac{1}{2} \times {d_1} \times {d_2}$ to establish a relation between both the diagonals.
$
   {A_r} = \dfrac{1}{2} \times {d_1} \times {d_2} \\ \Rightarrow
   2016{\text{ c}}{{\text{m}}^2} = \dfrac{1}{2} \times {d_1} \times {d_2} \\ \Rightarrow
   {d_1} \times {d_2} = 4032{\text{ c}}{{\text{m}}^2} - - - - (i) \\
 $
Now, following the property of the rhombus which states that the diagonals bisect each other at 90 degrees. So, here the diagonals ${d_1}$ and ${d_2}$ bisects each other at 90 degrees.

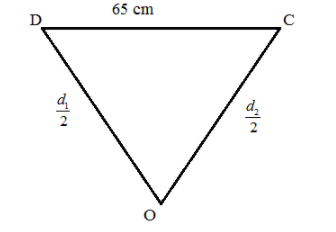
Applying Pythagoras theorem in the triangle ODC where DC is the hypotenuse and OD and OC are the base and the perpendicular of the triangle.
$
  {(hypotenuse)^2} = {(base)^2} + {(perpendicular)^2} \\ \Rightarrow
  {(DC)^2} = {\left( {OD} \right)^2} + {\left( {OC} \right)^2} - - - - (ii) \\
 $
Substituting the values of the sides from the figure shown in the equation (ii), we get
\[
  {(DC)^2} = {\left( {OD} \right)^2} + {\left( {OC} \right)^2} \\ \Rightarrow
  {(65)^2} = {\left( {\dfrac{{{d_1}}}{2}} \right)^2} + {\left( {\dfrac{{{d_2}}}{2}} \right)^2} \\ \Rightarrow
  4225 = \dfrac{{{d_1}^2 + {d_2}^2}}{4} \\ \Rightarrow
  {d_1}^2 + {d_2}^2 = 16900 - - - - (iii) \\
 \]
We know that, ${\left( {{d_1} + {d_2}} \right)^2} = {d_1}^2 + {d_2}^2 + 2{d_1}{d_2}$, substituting the known values in the equation we get
$
  {\left( {{d_1} + {d_2}} \right)^2} = {d_1}^2 + {d_2}^2 + 2{d_1}{d_2} \\ \Rightarrow
    16900 + 2\left( {4032} \right) \\
    16900 + 8064 \\ \Rightarrow
    24964 \\ \Rightarrow
  {d_1} + {d_2} = \sqrt {24964} \\ \Rightarrow
    158{\text{ cm}} - - - - (iv) \\
 $
Similarly, ${\left( {{d_1} - {d_2}} \right)^2} = {d_1}^2 + {d_2}^2 - 2{d_1}{d_2}$, substituting the known values in the equation, we get
$
  {\left( {{d_1} - {d_2}} \right)^2} = {d_1}^2 + {d_2}^2 - 2{d_1}{d_2} \\ \Rightarrow
    16900 - 2(4032) \\ \Rightarrow
    16900 - 8064 \\ \Rightarrow
    8836 \\ \Rightarrow
  {d_1} - {d_2} = \sqrt {8836} \\ \Rightarrow
    94{\text{ cm}} - - - - (v) \\
 $
Now, solving the equations (iv) and (v) to determine the length of the diagonals.
From the equation (iv), we get
$
  {d_1} + {d_2} = 158{\text{ cm}} \\ \Rightarrow
  {d_1} = 158 - {d_2} \\
 $
Substituting this value in the equation (v) we get
$
  {d_1} - {d_2} = 94{\text{ cm}} \\ \Rightarrow
  \left( {158 - {d_2}} \right) - {d_2} = 94 \\ \Rightarrow
   - 2{d_2} = 94 - 158 \\ \Rightarrow
  {d_2} = \dfrac{{64}}{2} \\ \Rightarrow
    32{\text{ cm}} \\
 $
Substituting the value of the length of the second diagonal as 32 cm in the equation ${d_1} = 158 - {d_2}$, we get
$
  {d_1} = 158 - {d_2} \\ \Rightarrow
   158 - 32 \\ \Rightarrow
   126{\text{ cm}} \\
 $
Hence, the length of the diagonals of the rhombus of the area 2016 square centimetre is 126 cm and 32 cm.

Option B is correct.

Note:
To solve these types of questions, students must know about the different properties and formulae of the rhombus. Moreover, there is a very slight difference between the rhombus and the square, in which diagonals in squares are equal while in rhombus are of different lengths.