Question

The area of a rhombus is 2016 sq.cm and its side is 65 cm. The lengths of the diagonal (in cm) respectively are
A.125, 35
B.136, 32
C.132, 26
D.135, 25

Answer 1

Hint: We have to find the diagonals of the rhombus. We have given the side and area of the rhombus. Firstly we will consider a rhombus and label it. Since the diagonals of rhombus bisect each other. So we have to calculate half of the diagonal from the right angled triangle formed In the figure. After calculating the half of diagonals. We can find the length of diagonals of the given rhombus .

Complete step-by-step answer:
Let ABCD be the given rhombus, AB, BC, CD and DA are the sides of rhombus . let the diagonals intersect each other at point O. Since the diagonal of rhombus bisect each other so, OA = OC and OB = OD.

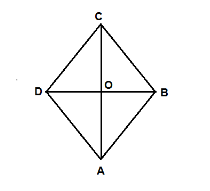
 Let the length of OC = x cm
Let the length of OB = y cm
Er have given the length of side of rhombus = 65cm
Also Area of rhombus = 2016sq. cm…………(i)
Area of rhombus = $ \dfrac{1}{2} \times AC \times DB $
 $ = \dfrac{1}{2} \times (AO + OC) \times (Bo + OD) $
 $ = \dfrac{1}{2} \times 2x \times 2y = 2xy $
So, Area of the rhombus = 2xy ………..(ii)
Equating (i) and(ii) we get
2xy = 2016 ………..(iii)
 $ \Rightarrow xy = 1008 $ ……………(iv)
Now form the figure BOC is a right angled triangle at B. so, by Pythagoras theorem
 $ B{C^2} = O{B^2} + O{C^2} $
BC is the side of rhombus, os BC = 65 OB = y and OC = x
 $ \therefore {65^2} = {y^2} + {x^2} $
 $ {x^2} + {y^2} = 4225 $ …………(v)
Adding equation (iii) and (v) we get
 $ {x^2} + {y^2} + 2xy = 2016 + 4225 $
 $ \therefore {(x + y)^2} = 6241 $ { using identity $ {x^2} + {y^2} + 2xy = {(x + y)^2} $ }
 $ x + y = \sqrt {6241} $
 $ x + y = 79 $ ……………….(vi)
Now from equation (iv) we can find y from x
 $ \therefore y = \dfrac{{1008}}{x} $ …………….(vii)
Putting value of equation (vii) in equation (vi)
 $ x + \dfrac{{1008}}{x} = 79 $
 $ \dfrac{{{x^2} + 1008}}{x} = 79 $
 $ {x^2} + 1008 = 79x $
 $ {x^2} - 79x + 1008 = 0 $
Applying quadratic formula
 $ x = \dfrac{{79 \pm \sqrt {{{(79)}^2} - 4 \times 1 \times 1008} }}{2} $
 $ = \dfrac{{79 \pm \sqrt {6241 - 4032} }}{2} $
 $ = \dfrac{{79 \pm \sqrt {2209} }}{2} $
 $ x = \dfrac{{79 \pm 47}}{2} $
 $ \Rightarrow x = \dfrac{{79 + 47}}{2},x = \dfrac{{79 - 47}}{2} $
 $ x = \dfrac{{126}}{2},\dfrac{{32}}{2} $
 $ x = 63,16 $
So, when x = 63, value of y = $ \dfrac{{1008}}{{63}} = 16 $
When x = 16, value of y $ = \dfrac{{1008}}{{16}} = 63 $
We get OC = 63 and OD = 16
AC= OA+OC = 63+63 = 126
BD = OB+OD = 16+16 = 32
So, diagonals of the rhombus are $ 126 $ cm and $ 32 $ cm. option (B) is correct.
So, the correct answer is “Option B”.

Note: A rhombus is flat shape with four equal sides. A rhombus looks like a diamond, all sides have equal length and opposite sides are parallel and opposite angles are equal .