Question

The area of a rectangular plot is 528 sq meter. The length of the plot (in meters) is one more than twice its breadth. We need to find the length and breadth of the plot.

Answer 1

Hint: In this problem, first we need to find the formula for the length in terms of the breadth of the rectangle. Next, use the formula for the area of a rectangle and substitute 528 for area. Then, solve the obtained quadratic equation.

Complete step by step answer:
Consider, the width and length of the plot be \[w\] and \[l\] respectively.

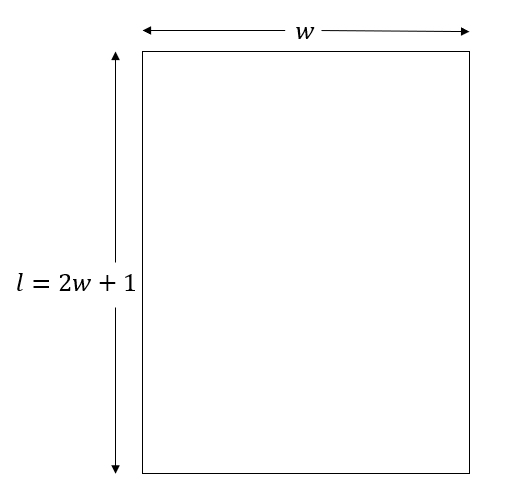
Since, the length of the plot is one more than twice its breadth, the length of the plot can be obtained as shown below.
\[l = 2w + 1\]
Now, the formula for the area \[A\] of a rectangle having length \[l\] and width \[w\] is shown below.
\[A = l \times w\]
Now, the area of the rectangular plot is 528 sq. meter, therefore, substitute 528 for \[A\] and \[2w + 1\] for \[l\] in the above formula.
\[
  \,\,\,\,\,528 = \left( {2w + 1} \right) \times w \\
   \Rightarrow 528 = 2{w^2} + w \\
   \Rightarrow 2{w^2} + w - 528 = 0 \\
   \Rightarrow 2{w^2} + \left( {33 - 32} \right)w - 528 = 0 \\
   \Rightarrow 2{w^2} - 32w + 33w - 528 = 0 \\
\]
Further, solve the above quadratic equation.
\[
  \,\,\,\,\,\,2w\left( {w - 16} \right) + 33\left( {w - 16} \right) = 0 \\
   \Rightarrow \left( {2w + 33} \right)\left( {w - 16} \right) = 0 \\
   \Rightarrow w = - \dfrac{{33}}{2}m\,\,{\text{or}}\,\,16m \\
\]
Since, the breadth of the rectangular plot cannot be negative; the breadth of the plot will be 16 meter.
Now, substitute 16 for \[w\] in the formula for length \[l = 2w + 1\] to obtain the value of the length.
\[
  \,\,\,\,\,\,l = 2\left( {16} \right) + 1 \\
   \Rightarrow l = 32 + 1 \\
   \Rightarrow l = 33m \\
\]

Thus, the breadth of the plot is 16 meters and length of the plot is 33 meters.

Note: The breadth and length of the rectangle must be in a single variable. While solving the obtained quadratic equation, if it is difficult to solve using middle term factorisation, we can use quadratic formula also.