Question

The area of a parallelogram is \[24{\text{ }}c{m^2}\] and the base of the parallelogram is \[6{\text{ }}cm\]. What is the height of the parallelogram?

Answer 1

Hint: Given, the area of a parallelogram is \[24{\text{ }}c{m^2}\] and the base of the parallelogram is \[6{\text{ }}cm\]. As we know, the area of a parallelogram is given by \[\left( {{\text{base}} \times {\text{height}}} \right)\]. We will put the given values of area of the parallelogram and length of the base in the formula then we will simplify it to find the height of the parallelogram.

Complete step by step answer:
As we know, a parallelogram is a two-dimensional figure with four sides. A parallelogram has two pairs of parallel sides with equal measures.
Given, a parallelogram of area \[24{\text{ }}c{m^2}\] and the base of the parallelogram is \[6{\text{ }}cm\].
The parallelogram be \[ABCD\] as shown in the figure,

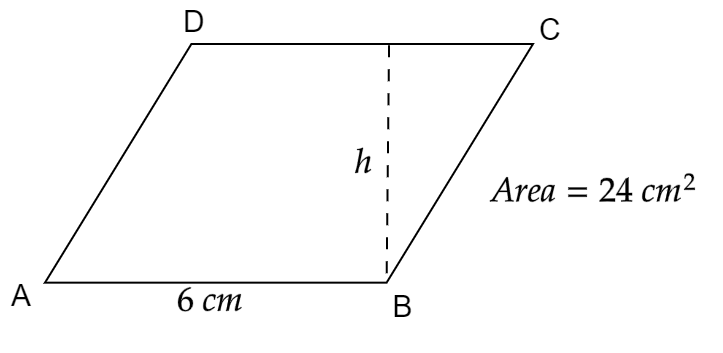
Here, \[AB\] is the base of \[6{\text{ }}cm\] and the height be \[h\].
As we know that \[{\text{Area of a parallelogram}} = {\text{base}} \times {\text{height}}\]
So, for the given parallelogram, we have
\[ \Rightarrow {\text{Area of the parallelogram}} = AB \times h\]
Putting the values, we get
\[ \Rightarrow 24{\text{ }}c{m^2} = 6{\text{ }}cm \times h\]
On simplification, we get
\[ \Rightarrow h = \dfrac{{24{\text{ }}c{m^2}}}{{6{\text{ }}cm}}\]
On calculating, we get
\[ \Rightarrow h = 4{\text{ }}cm\]
Therefore, the height of the parallelogram is \[4{\text{ }}cm\].

Note:
The other ways that we can use in different problems to calculate the area of a parallelogram are:
\[(1)\] The area is \[\left( {\dfrac{1}{2} \times {d_1} \times {d_2}\sin x} \right)\], if the length of two diagonal is given as \[{d_1}\], \[{d_2}\] and the angle between them is \[x\].
\[(2)\] If the length of two sides of a parallelogram is known and angle between any two sides is known then the area is \[\left( {ab\sin x} \right)\]. Here, \[a\], \[b\] is the length of two adjacent sides and \[x\] is the angle between them.