Question

The area of $ 4 $ walls of a room is $ 520\,{m^2} $ while its length and breadth are $ 15,\,\,and\,\,11m $ respectively. Find the length of longest rod that can fit in the room and volume of room

Answer 1

Hint: For given problem we first find height of the room by substituting value of given length, breadth in area of four walls of room and then using length of height so obtained along with length, breadth we can find volume and length of longest rod by using standard formulas of mensuration for cuboid.
 Length of longest rod = $ \sqrt {{L^2} + {B^2} + {H^2}} $ and Volume of room = $ L.B.H. $ , where L, B, and H are length, breadth and height of the room.

Complete step-by-step answer:
Given,
Length of room = $ 15\,m $ .
Breadth of the room = $ 11\,m $
Area of the four walls = $ 520\,{m^2} $

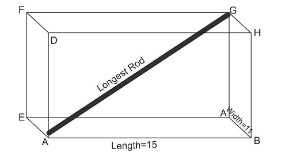
Let height of the room = H
We know that area of four wall of the room is given as: $ 2H\left( {L + B} \right) $
Substituting values in above formulas. We have,
 $
  520 = 2\left( {15 + 11} \right) \times H \\
   \Rightarrow 520 = 2 \times 26 \times H \\
   \Rightarrow 520 = 52H \\
   \Rightarrow H = \dfrac{{520}}{{52}} \\
   \Rightarrow H = 10 \;
  $
Therefore, from above we see that the height of the room is $ 10m $ .
Also, we know that the length of the longest rod is given as: $ \sqrt {{L^2} + {B^2} + {H^2}} $ .
Substituting values of length, breadth and height in above. We have,
Length of longest rod = $ \sqrt {{{\left( {15} \right)}^2} + {{\left( {11} \right)}^2} + {{\left( {10} \right)}^2}} $
Length of longest rod = $ \sqrt {225 + 121 + 100} $
Length of longest rod = $ \sqrt {446} $
Hence, the length of the longest rod that can be placed inside the room is $ \sqrt {446} \,\,m $ .
Now, we will find the volume of the room.
We know that volume of a room (cuboid shape) = $ L \times B \times H $
Substituting values in above. We have,
 $
  Volume(V) = 15 \times 11 \times 10 \\
  Volume(V) = 1650 \;
 $
Hence, the volume of the room is $ 1650\,\,{m^3} $ .

Note: In mensuration there are different formulas for different figures even there are different formulas for surface area and volumes of figures. So, to get the right solution of the problem students should select appropriate formulas and also do calculations very carefully to get the required solution of the problem.