Question

The area bounded by the curves \[y = {x^2}\] and \[y = 1 - {x^2}\] is
(a) \[\dfrac{{\sqrt 8 }}{3}\]
(b) \[\dfrac{{16}}{3}\]
(c) \[\dfrac{{32}}{3}\]
(d) \[\dfrac{{17}}{3}\]

Answer 1

Hint: Here, we need to find the area bounded by the two curves. First, we will find the points of intersection of the curves. Then, we will graph the curves to find the area bounded by the curves. Finally, we will use integration to find the areas required, and subtract them to find the area bounded by the curves \[y = {x^2}\] and \[y = 1 - {x^2}\] in square units.

Formula Used:
 We will use the following formulas:
1.The sum of two integrals \[f\left( x \right)\] and \[g\left( x \right)\] can be written as \[\int {f\left( x \right)} dx + \int {g\left( x \right)} dx = \int {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx\].
2.The integral of a function of the form \[af\left( x \right)\] can be written as \[\int {af\left( x \right)} dx = a\int {f\left( x \right)} dx\].
3.The integral of a function of the form \[{x^n}\] can be written as \[\int {{x^n}} dx = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C\].

Complete step-by-step answer:
First, we will find the point of intersection of the given curves.
Substituting \[y = {x^2}\] in the equation \[y = 1 - {x^2}\], we get
\[ \Rightarrow {x^2} = 1 - {x^2}\]
Adding \[{x^2}\] on both sides , we get
\[\begin{array}{l} \Rightarrow {x^2} + {x^2} = 1 - {x^2} + {x^2}\\ \Rightarrow 2{x^2} = 1\end{array}\]
Dividing both sides by 2, we get
\[ \Rightarrow {x^2} = \dfrac{1}{2}\]
Taking the square root on both sides, we get
\[\begin{array}{l} \Rightarrow x = \pm \sqrt {\dfrac{1}{2}} \\ \Rightarrow x = \pm \dfrac{1}{{\sqrt 2 }}\\ \Rightarrow x = \dfrac{1}{{\sqrt 2 }}, - \dfrac{1}{{\sqrt 2 }}\end{array}\]
Substituting \[x = \dfrac{1}{{\sqrt 2 }}\] in the equation \[y = {x^2}\], we get
\[ \Rightarrow y = {\left( {\dfrac{1}{{\sqrt 2 }}} \right)^2}\]
Simplifying the expression, we get
\[ \Rightarrow y = \dfrac{1}{2}\]
Thus, we get one point of intersection of the two equations as \[\left( {\dfrac{1}{{\sqrt 2 }},\dfrac{1}{2}} \right)\].
Substituting \[x = - \dfrac{1}{{\sqrt 2 }}\] in the equation \[y = {x^2}\], we get
\[ \Rightarrow y = {\left( { - \dfrac{1}{{\sqrt 2 }}} \right)^2}\]
Simplifying the expression, we get
\[ \Rightarrow y = \dfrac{1}{2}\]
Thus, we get the second point of intersection of the two equations as \[\left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{1}{2}} \right)\].
Now, we will draw the graphs of the two curves and find the bounded region.
Drawing the two curves \[y = {x^2}\] and \[y = 1 - {x^2}\] on the same graph, we get

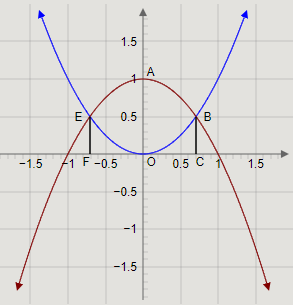
Here, the region ABOE is the region bounded by the two curves. E and B are the points of intersection \[\left( {\dfrac{1}{{\sqrt 2 }},\dfrac{1}{2}} \right)\] and \[\left( { - \dfrac{1}{{\sqrt 2 }},\dfrac{1}{2}} \right)\] respectively.
Since the curves are symmetrical about the \[y - \]axis, the regions ABO and AEO have the same area.
The area of the region ABO is the difference in the areas of the region ABCO, and the region BCO.
We will use integration to calculate the area under the curves.
First, we will find the area of the region ABCO.
The region ABCO lies under the curve \[y = 1 - {x^2}\] between the values 0 and \[\dfrac{1}{{\sqrt 2 }}\] on the \[x - \]axis.
Therefore, we get
Area of the region ABCO \[ = \int\limits_0^{\dfrac{1}{{\sqrt 2 }}} {\left( {1 - {x^2}} \right)} dx\]
The sum of two integrals \[f\left( x \right)\] and \[g\left( x \right)\] can be written as \[\int {f\left( x \right)} dx + \int {g\left( x \right)} dx = \int {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx\].
Therefore, using the property \[\int {\left[ {f\left( x \right) + g\left( x \right)} \right]} dx = \int {f\left( x \right)} dx + \int {g\left( x \right)} dx\], we get
\[ \Rightarrow \] Area of the region ABCO \[ = \int\limits_0^{\dfrac{1}{{\sqrt 2 }}} {\left( 1 \right)} dx + \int\limits_0^{\dfrac{1}{{\sqrt 2 }}} {\left( { - {x^2}} \right)} dx\]
The integral of a function of the form \[af\left( x \right)\] can be written as \[\int {af\left( x \right)} dx = a\int {f\left( x \right)} dx\].
\[ \Rightarrow \] Area of the region ABCO \[ = \int\limits_0^{\dfrac{1}{{\sqrt 2 }}} {\left( 1 \right)} dx - \int\limits_0^{\dfrac{1}{{\sqrt 2 }}} {\left( {{x^2}} \right)} dx\]
The integral of a function of the form \[{x^n}\] can be written as \[\int {{x^n}} dx = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C\].
The integral of a constant with respect to a variable is the variable itself.
Therefore, we get
\[ \Rightarrow \] Area of the region ABCO \[ = \left. {\left( x \right)} \right|_0^{\dfrac{1}{{\sqrt 2 }}} - \left. {\left( {\dfrac{{{x^{2 + 1}}}}{{2 + 1}}} \right)} \right|_0^{\dfrac{1}{{\sqrt 2 }}} = \left. {\left( x \right)} \right|_0^{\dfrac{1}{{\sqrt 2 }}} - \left. {\left( {\dfrac{{{x^3}}}{3}} \right)} \right|_0^{\dfrac{1}{{\sqrt 2 }}}\]
Substituting the limits, we get
\[ \Rightarrow \] Area of the region ABCO \[ = \dfrac{1}{{\sqrt 2 }} - 0 - \dfrac{{{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^3}}}{3} + \dfrac{{{{\left( 0 \right)}^3}}}{3}\]
Simplifying the expression, we get
\[ \Rightarrow \] Area of the region ABCO \[ = \dfrac{1}{{\sqrt 2 }} - 0 - \dfrac{{\dfrac{1}{{2\sqrt 2 }}}}{3} + 0 = \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{6\sqrt 2 }} = \dfrac{6}{{6\sqrt 2 }} - \dfrac{1}{{6\sqrt 2 }} = \dfrac{5}{{6\sqrt 2 }}\]
Rationalising the denominator, we get
\[ \Rightarrow \] Area of the region ABCO \[ = \dfrac{5}{{6\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = \dfrac{{5\sqrt 2 }}{{12}}\]………..\[\left( 1 \right)\]
Now, we will find the area of the region BCO.
The region BCO lies under the curve \[y = {x^2}\] between the values 0 and \[\dfrac{1}{{\sqrt 2 }}\] on the \[x - \]axis.
Therefore, we get
Area of the region BCO \[ = \int\limits_0^{\dfrac{1}{{\sqrt 2 }}} {\left( {{x^2}} \right)} dx\]
Using the property \[\int {{x^n}} dx = \dfrac{{{x^{n + 1}}}}{{n + 1}} + C\], we get
\[ \Rightarrow \] Area of the region BCO \[ = \left. {\left( {\dfrac{{{x^{2 + 1}}}}{{2 + 1}}} \right)} \right|_0^{\dfrac{1}{{\sqrt 2 }}} = \left. {\left( {\dfrac{{{x^3}}}{3}} \right)} \right|_0^{\dfrac{1}{{\sqrt 2 }}}\]
Substituting the limits, we get
\[ \Rightarrow \] Area of the region BCO \[ = \dfrac{{{{\left( {\dfrac{1}{{\sqrt 2 }}} \right)}^3}}}{3} - \dfrac{{{{\left( 0 \right)}^3}}}{3}\]
Simplifying the expression, we get
\[ \Rightarrow \] Area of the region BCO \[ = \dfrac{{\dfrac{1}{{2\sqrt 2 }}}}{3} - 0 = \dfrac{1}{{6\sqrt 2 }}\]
Rationalising the denominator, we get
\[ \Rightarrow \] Area of the region BCO \[ = \dfrac{1}{{6\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} = \dfrac{{\sqrt 2 }}{{12}}\]……….\[\left( 2 \right)\]
Now, we will find the area of the region ABO.
The area of the region ABO is the difference in the areas of the region ABCO, and the region BCO.
Therefore, we get
Area of region ABO \[ = \dfrac{{5\sqrt 2 }}{{12}} - \dfrac{{\sqrt 2 }}{{12}}\]
Subtracting the terms, we get
\[ \Rightarrow \] Area of region ABO \[ = \dfrac{{4\sqrt 2 }}{{12}} = \dfrac{{\sqrt 2 }}{3}\]
Since the curves are symmetrical about the \[y - \]axis, the regions ABO and AEO have the same area.
Therefore, we get the area of the required region as
Area of region ABOE \[ = 2 \times \]Area of the region ABO
Thus, we get
\[ \Rightarrow \]Area of region ABOE \[ = 2 \times \dfrac{{\sqrt 2 }}{3} = \dfrac{{2\sqrt 2 }}{3}\]
Rewriting the expression, we get
\[ \Rightarrow \] Area of region ABOE \[ = \dfrac{{\sqrt 4 \sqrt 2 }}{3} = \dfrac{{\sqrt 8 }}{3}\]
Therefore, the area bounded by the two given curves is \[\dfrac{{\sqrt 8 }}{3}\] square units.
Thus, the correct option is option (a).

Note: Here, we can make a mistake by using the ordinates of the point of intersection, that is \[\dfrac{1}{2}\] as a limit in the integral, which is incorrect. We only need to use the \[x\] coordinates because we are integrating with respect to \[x\] to find the area of the region under the curve. We need to also know the different formulas of integration to carry out integration easily. Sometimes, we integrate the function but forget to substitute the values. Hence, we get the wrong answer