
The area bounded by the curves y = cos x and y = sin x between the ordinates, x = 0 and x = $\dfrac{{3\pi }}{2}$.
$\left( a \right)4\sqrt 2 + 2$
$\left( b \right)4\sqrt 2 - 1$
$\left( c \right)4\sqrt 2 + 1$
$\left( d \right)4\sqrt 2 - 2$
Answer
582.3k+ views
Hint: In this particular question first draw the pictorial representation of the above problem it will give us a clear picture of what we have to find out, then use the concept of area under the curve by integration method which is given as $A = \int_{x = {x_1}}^{x = {x_2}} {\left( {{y_1} - {y_2}} \right)dx} $, where ${y_1}{\text{ and }}{y_2}$ are the upper and lower curves and ${x_1}{\text{ and }}{x_2}$ are the upper and lower limits so use these concepts to reach the solution of the question.
Complete step by step answer:
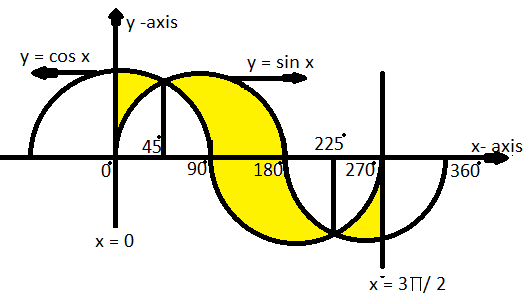
The area bounded by the curves y = cos x and y = sin x between the ordinates, x = 0 and x = $\dfrac{{3\pi }}{2}$ is shown above by the yellow color.
Now as we know that to calculate the area under the curves the simplest method is by integration method, which is given as, $A = \int_{x = {x_1}}^{x = {x_2}} {\left( {{y_1} - {y_2}} \right)dx} $, where ${y_1}{\text{ and }}{y_2}$ are the upper and lower curves and ${x_1}{\text{ and }}{x_2}$ are the upper and lower limits.
Now as we know that sin x and cos x in a complete cycle are equal at 45 degrees and 225 degrees.
$ \Rightarrow {45^o} = \dfrac{\pi }{4},{225^o} = \dfrac{{5\pi }}{4}$
So the integration is break into three parts, in first and third part upper curve is cos x and lower curve is sin x and in second part upper curve is sin x and lower curve is cos x, so the required area is,
$A = \int_{x = 0}^{x = \dfrac{\pi }{4}} {\left( {\cos x - \sin x} \right)dx} + \int_{x = \dfrac{\pi }{4}}^{x = \dfrac{{5\pi }}{4}} {\left( {\sin x - \cos x} \right)dx} + \int_{x = \dfrac{{5\pi }}{4}}^{x = \dfrac{{3\pi }}{2}} {\left( {\cos x - \sin x} \right)dx} $
Now as we know that $\int {\sin xdx = - \cos x + c,\int {\cos xdx = \sin x + c} } $, where c is some arbitrary integration constant so use this in the above integral we have,
$ \Rightarrow A = \left[ {\sin x - \left( { - \cos x} \right)} \right]_0^{\dfrac{\pi }{4}} + \left[ { - \cos x - \sin x} \right]_{\dfrac{\pi }{4}}^{\dfrac{{5\pi }}{4}} + \left[ {\sin x - \left( { - \cos x} \right)} \right]_{\dfrac{{5\pi }}{4}}^{\dfrac{{3\pi }}{2}}$
$ \Rightarrow A = \left[ {\sin x + \cos x} \right]_0^{\dfrac{\pi }{4}} - \left[ {\cos x + \sin x} \right]_{\dfrac{\pi }{4}}^{\dfrac{{5\pi }}{4}} + \left[ {\sin x + \cos x} \right]_{\dfrac{{5\pi }}{4}}^{\dfrac{{3\pi }}{2}}$
Now apply integration limits we have,
\[ \Rightarrow A = \left[ {\sin \dfrac{\pi }{4} + \cos \dfrac{\pi }{4} - \sin 0 - \cos 0} \right] - \left[ {\sin \dfrac{{5\pi }}{4} + \cos \dfrac{{5\pi }}{4} - \sin \dfrac{\pi }{4} - \cos \dfrac{\pi }{4}} \right] + \left[ {\sin \dfrac{{3\pi }}{2} + \cos \dfrac{{3\pi }}{2} - \sin \dfrac{{5\pi }}{4} - \cos \dfrac{{5\pi }}{4}} \right]\]
Now as we know that, $\sin \dfrac{\pi }{4} = \cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$, $\sin \dfrac{{5\pi }}{4} = \cos \dfrac{{5\pi }}{4} = - \dfrac{1}{{\sqrt 2 }}$, $\sin \dfrac{{3\pi }}{2} = - 1,\cos \dfrac{{3\pi }}{2} = 0$, and sin 0 = 0, cos 0 = 1, so use these values in the above equation we have,
\[ \Rightarrow A = \left[ {\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} - 0 - 1} \right] - \left[ { - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }}} \right] + \left[ { - 1 + 0 - \left( { - \dfrac{1}{{\sqrt 2 }}} \right) - \left( { - \dfrac{1}{{\sqrt 2 }}} \right)} \right]\]
Now simplify we have,
\[ \Rightarrow A = \left[ {\dfrac{2}{{\sqrt 2 }} - 1} \right] - \left[ { - \dfrac{4}{{\sqrt 2 }}} \right] + \left[ { - 1 + \dfrac{2}{{\sqrt 2 }}} \right]\]
\[ \Rightarrow A = \left[ {\dfrac{8}{{\sqrt 2 }} - 2} \right]\]
\[ \Rightarrow A = \left[ {\dfrac{8}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} - 2} \right]\]
\[ \Rightarrow A = 4\sqrt 2 - 2\] Sq. units.
So this is the required area bounded by the given curves.
So, the correct answer is “Option D”.
Note: Whenever we face such types of questions the key concept we have to remember is that always recall the basic integration formula such as, $\int {\sin xdx = - \cos x + c,\int {\cos xdx = \sin x + c} } $, where c is some arbitrary integration constant and the formula of area under the curve using integration method which is stated above.
Complete step by step answer:
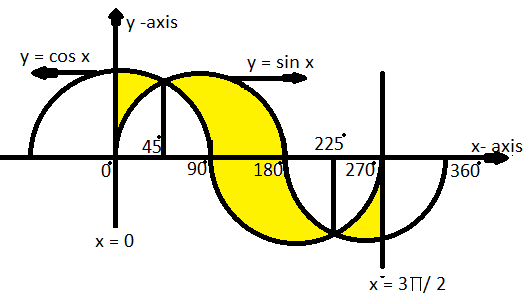
The area bounded by the curves y = cos x and y = sin x between the ordinates, x = 0 and x = $\dfrac{{3\pi }}{2}$ is shown above by the yellow color.
Now as we know that to calculate the area under the curves the simplest method is by integration method, which is given as, $A = \int_{x = {x_1}}^{x = {x_2}} {\left( {{y_1} - {y_2}} \right)dx} $, where ${y_1}{\text{ and }}{y_2}$ are the upper and lower curves and ${x_1}{\text{ and }}{x_2}$ are the upper and lower limits.
Now as we know that sin x and cos x in a complete cycle are equal at 45 degrees and 225 degrees.
$ \Rightarrow {45^o} = \dfrac{\pi }{4},{225^o} = \dfrac{{5\pi }}{4}$
So the integration is break into three parts, in first and third part upper curve is cos x and lower curve is sin x and in second part upper curve is sin x and lower curve is cos x, so the required area is,
$A = \int_{x = 0}^{x = \dfrac{\pi }{4}} {\left( {\cos x - \sin x} \right)dx} + \int_{x = \dfrac{\pi }{4}}^{x = \dfrac{{5\pi }}{4}} {\left( {\sin x - \cos x} \right)dx} + \int_{x = \dfrac{{5\pi }}{4}}^{x = \dfrac{{3\pi }}{2}} {\left( {\cos x - \sin x} \right)dx} $
Now as we know that $\int {\sin xdx = - \cos x + c,\int {\cos xdx = \sin x + c} } $, where c is some arbitrary integration constant so use this in the above integral we have,
$ \Rightarrow A = \left[ {\sin x - \left( { - \cos x} \right)} \right]_0^{\dfrac{\pi }{4}} + \left[ { - \cos x - \sin x} \right]_{\dfrac{\pi }{4}}^{\dfrac{{5\pi }}{4}} + \left[ {\sin x - \left( { - \cos x} \right)} \right]_{\dfrac{{5\pi }}{4}}^{\dfrac{{3\pi }}{2}}$
$ \Rightarrow A = \left[ {\sin x + \cos x} \right]_0^{\dfrac{\pi }{4}} - \left[ {\cos x + \sin x} \right]_{\dfrac{\pi }{4}}^{\dfrac{{5\pi }}{4}} + \left[ {\sin x + \cos x} \right]_{\dfrac{{5\pi }}{4}}^{\dfrac{{3\pi }}{2}}$
Now apply integration limits we have,
\[ \Rightarrow A = \left[ {\sin \dfrac{\pi }{4} + \cos \dfrac{\pi }{4} - \sin 0 - \cos 0} \right] - \left[ {\sin \dfrac{{5\pi }}{4} + \cos \dfrac{{5\pi }}{4} - \sin \dfrac{\pi }{4} - \cos \dfrac{\pi }{4}} \right] + \left[ {\sin \dfrac{{3\pi }}{2} + \cos \dfrac{{3\pi }}{2} - \sin \dfrac{{5\pi }}{4} - \cos \dfrac{{5\pi }}{4}} \right]\]
Now as we know that, $\sin \dfrac{\pi }{4} = \cos \dfrac{\pi }{4} = \dfrac{1}{{\sqrt 2 }}$, $\sin \dfrac{{5\pi }}{4} = \cos \dfrac{{5\pi }}{4} = - \dfrac{1}{{\sqrt 2 }}$, $\sin \dfrac{{3\pi }}{2} = - 1,\cos \dfrac{{3\pi }}{2} = 0$, and sin 0 = 0, cos 0 = 1, so use these values in the above equation we have,
\[ \Rightarrow A = \left[ {\dfrac{1}{{\sqrt 2 }} + \dfrac{1}{{\sqrt 2 }} - 0 - 1} \right] - \left[ { - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }} - \dfrac{1}{{\sqrt 2 }}} \right] + \left[ { - 1 + 0 - \left( { - \dfrac{1}{{\sqrt 2 }}} \right) - \left( { - \dfrac{1}{{\sqrt 2 }}} \right)} \right]\]
Now simplify we have,
\[ \Rightarrow A = \left[ {\dfrac{2}{{\sqrt 2 }} - 1} \right] - \left[ { - \dfrac{4}{{\sqrt 2 }}} \right] + \left[ { - 1 + \dfrac{2}{{\sqrt 2 }}} \right]\]
\[ \Rightarrow A = \left[ {\dfrac{8}{{\sqrt 2 }} - 2} \right]\]
\[ \Rightarrow A = \left[ {\dfrac{8}{{\sqrt 2 }} \times \dfrac{{\sqrt 2 }}{{\sqrt 2 }} - 2} \right]\]
\[ \Rightarrow A = 4\sqrt 2 - 2\] Sq. units.
So this is the required area bounded by the given curves.
So, the correct answer is “Option D”.
Note: Whenever we face such types of questions the key concept we have to remember is that always recall the basic integration formula such as, $\int {\sin xdx = - \cos x + c,\int {\cos xdx = \sin x + c} } $, where c is some arbitrary integration constant and the formula of area under the curve using integration method which is stated above.
Recently Updated Pages
Master Class 12 Business Studies: Engaging Questions & Answers for Success

Master Class 12 Economics: Engaging Questions & Answers for Success

Master Class 12 English: Engaging Questions & Answers for Success

Master Class 12 Maths: Engaging Questions & Answers for Success

Master Class 12 Social Science: Engaging Questions & Answers for Success

Master Class 12 Chemistry: Engaging Questions & Answers for Success

Trending doubts
What are the major means of transport Explain each class 12 social science CBSE

Which are the Top 10 Largest Countries of the World?

Draw a labelled sketch of the human eye class 12 physics CBSE

Explain sex determination in humans with line diag class 12 biology CBSE

The pH of the pancreatic juice is A 64 B 86 C 120 D class 12 biology CBSE

Give 10 examples of unisexual and bisexual flowers




