Question

The area bounded by the curve ${{x}^{2}}+2x+y-3=0$ , the x-axis and the tangent at the point, where it meets the y-axis is_________.

Answer 1

Hint: Reduce the curve into standard form and identify the type of curve and draw its graph and determine the point where tangent cuts the x axis and then use the method of integration for the area bounded by the curve.

Complete step by step answer:
Let us consider the curve, ${{x}^{2}}+2x+y-3=0$. Using completing the square method to solve it further, we get
$\begin{align}
  & {{(x+1)}^{2}}-1+y-3=0 \\
 & {{(x+1)}^{2}}=-y+4 \\
 & {{(x+1)}^{2}}=-(y-4) \\
\end{align}$
We know the standard form of a parabola is given by ${{(x-h)}^{2}}=4a(y-k)$, where focus is at $(h,k+a)$ and vertex at $(h,k)$.
So on comparing ${{(x+1)}^{2}}=-(y-4)$ with the standard equation of the parabola, we can write it as ${{(x-h)}^{2}}=4a(y-k)$. Then, the curve will be a parabola whose vertex at $(-1,4)$.
Now the given parabola cuts the $x$ axis at a point, when y coordinates of curve $=0$.
${{x}^{2}}+2x+y-3=0$
$\begin{align}
  & {{x}^{2}}+2x+0-3=0 \\
 & {{x}^{2}}+2x-3=0 \\
\end{align}$
Now factorize it using middle term splitting,
${{x}^{2}}+3x-x-3=0$
$x(x+3)-1(x+3)=0$
Taking $(x+3)$ common, we get
$(x+3)(x-1)=0$
$x=1$ and $x=-3$
So, points on the x-axis are $(1,0) \And (-3,0)$. Plotting the curve, we get,

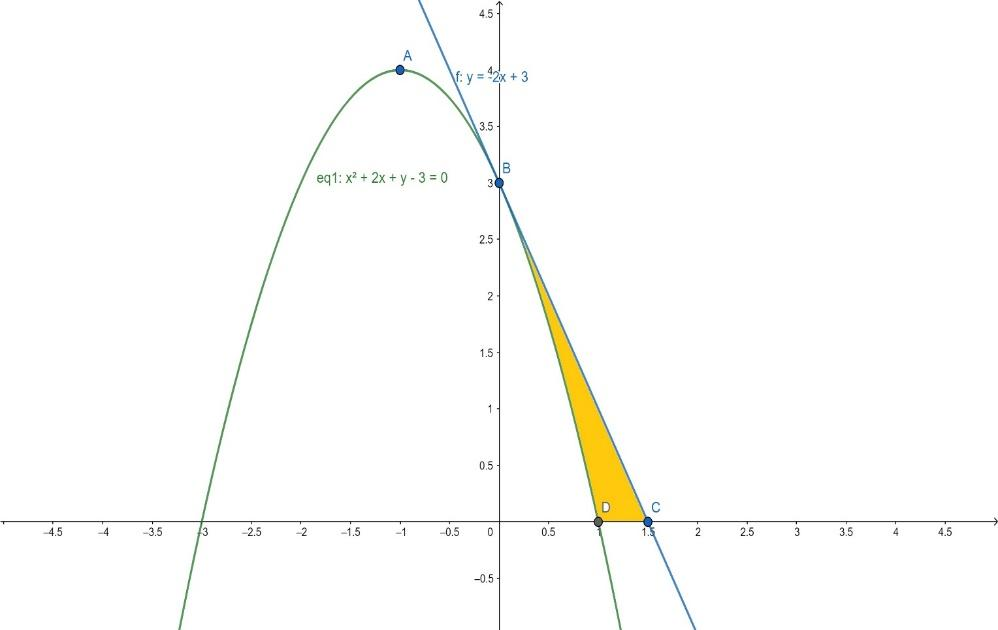
Now we need to find the equation of tangent. We know the given point of a tangent is the point where the curve cuts the y-axis. So to find the point on y-axis x coordinate must be zero.
${{x}^{2}}+2x+y-3=0$
$y=3$
Given point $(0,3)$ of the tangent. We have to find a tangent to the curve ${{x}^{2}}+2x+y-3=0$. We can rearrange it in form, $y=-{{x}^{2}}-2x+3$.
We need to find the slope of tangent and we know that slope of tangent through a curve is equal to $\dfrac{dy}{dx}$ at the given point. We know that $\dfrac{d{{x}^{n}}}{dx}=n{{x}^{n-1}}$, so,
$\dfrac{dy}{dx}=-\left( 2x+2 \right)$ at $(0,3)$
At $x=0$, we get
$\dfrac{dy}{dx}=-2$
We know the equation of the tangent is $(y-{{y}_{1}})=m(x-{{x}_{1}})$, where m is the slope and ${{x}_{1}}\And {{y}_{1}}$ are given points of the tangent. Then, we can write the equation as:
$\begin{align}
  & (y-3)=-2(x-0) \\
 & y=-2x+3 \\
\end{align}$
We draw it on the graph as well as. We need to find a point where tangent cuts the x-axis.
Coordinate y=0, we have
$\begin{align}
  & 0=-2x+3 \\
 & x=\dfrac{3}{2} \\
\end{align}$
It cuts the x-axis at $\left( \dfrac{3}{2},0 \right)$.
By observing the graph, the required area bounded by curve and tangent is shown using dark colour. We use integration w.r.t. x axis.
Required area \[=\int\limits_{0}^{\dfrac{3}{2}}{{{y}_{line}}dx-\int\limits_{0}^{1}{{{y}_{curve}}dx}}\]
$=\int\limits_{0}^{\dfrac{3}{2}}{(-2x+3)dx-\int\limits_{0}^{1}{(-{{x}^{2}}-2x+3)dx}}$
We know that $\int{{{x}^{n}}dx=\dfrac{{{x}^{n+1}}}{n+1}}$, so we get
$\begin{align}
  & =\left[ -{{x}^{2}}+3x \right]_{0}^{^{\dfrac{3}{2}}}-\left[ -\dfrac{{{x}^{3}}}{3}-{{x}^{2}}+3x \right]_{0}^{1} \\
 & =\left[ -\dfrac{9}{4}+\dfrac{9}{2}-0-0 \right]-\left[ -\dfrac{1}{3}-1+3-0-0 \right] \\
\end{align}$
$\begin{align}
  & =-\dfrac{9}{4}+\dfrac{9}{2}+\dfrac{1}{3}+1-3 \\
 & =\dfrac{7}{12}sq.unit \\
\end{align}$
The area bounded by the curve ${{x}^{2}}+2x+y-3=0$, the x-axis and the tangent at the point, where it meets the y-axis $=\dfrac{7}{12}sq.unit$.

Note: Constructing the graph of the curve is necessary for proper understanding. In this question, it is necessary to manipulate the curve equation in the standard form to get the resulting curve. And another alternate method which can be used is by integrating the function over the y-axis rather than x-axis. However, it is used when the function is given in terms of $y$ and we are having value of $y$ ordinate, in this case we use $dy$ instead of $dx$.