Question

The area and height of the trapezium are $34c{m^2}$ and 4cm. One of its parallel sides is 10cm. Find the length of the other parallel side.

Answer 1

Hint: The area and height of the trapezium given are $34c{m^2}$ and 4cm and length of one of its parallel sides is 10cm. Use the area of trapezium formula $\dfrac{1}{2}h\left( {a + b} \right)$, where h is the height of the trapezium, a and b are the lengths of the parallel sides of the trapezium. Substitute the values of area, height and one parallel side to find the length of another parallel side.

Complete step-by-step answer:

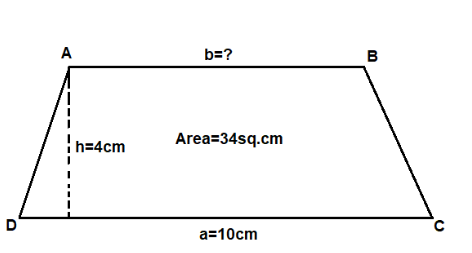
We are given that the area and height of the trapezium are $34c{m^2}$ and 4cm. One of its parallel sides is 10cm.
We have to find the length of another parallel side.
We are given the area of the trapezium is $34c{m^2}$
Formula to find area of the trapezium is $\dfrac{1}{2}h\left( {a + b} \right)$
$ \to \dfrac{1}{2}h\left( {a + b} \right) = 34$
We already know the values of a, h. We have to find the value of b.
Substitute the values of a, h in $\dfrac{1}{2}h\left( {a + b} \right)$
$
  \dfrac{1}{2}h\left( {a + b} \right) = 34 \\
  h = 4cm,a = 10cm \\
   \to \dfrac{1}{2} \times 4 \times \left( {10 + b} \right) = 34 \\
   \to 4 \times \left( {10 + b} \right) = 34 \times 2 = 68 \\
   \to 10 + b = \dfrac{{68}}{4} \\
   \to 10 + b = 17 \\
  \therefore b = 17 - 10 = 7cm \\
 $
The length of another parallel side is 7cm.

Note: A trapezium is a quadrilateral which has one parallel pair of sides and one non-parallel pair of sides. Square, rectangle and parallelogram can also be called trapeziums because they all have one pair of parallel sides irrespective of the other pair. A trapezium has only one pair of parallel sides and a parallelogram has two pairs of parallel sides. The opposite sides in a parallelogram are parallel and equal whereas they are unequal in a trapezium. As the trapezium has one pair of parallel sides do not confuse it with a parallelogram.