Question

The angles of the triangle are in ratio \[1:2:3\] . Find the difference between smallest and largest angle (in degrees).

Answer 1

Hint:
If the angles are in ratio \[1:2:3\], then we will write this ratio in terms of x and apply angle sum property and then we will find the value of x. Here, x will be the smallest angle and 3x will be the largest angle. For finding the difference between the smallest and largest angles, subtract the smallest angle from the largest angle.

Complete step by step solution:
Given, the angles of the triangle are in ratio \[1:2:3\] .
If we write this ratio in terms of,
Let the angles be x, 2x and 3x.

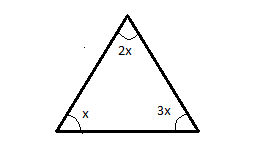
Now we apply angle sum property.
According to angle sum property, the sum of all angles of a triangle is \[{180^ \circ }\] .
Therefore,
 \[x + 2x + 3x = {180^ \circ }\]
On adding like terms, we get
 \[ \Rightarrow 6x = {180^ \circ }\]
On dividing by 6, we get
 \[ \Rightarrow x = \dfrac{{{{180}^ \circ }}}{6}\]
On simplification, we get
 \[ \Rightarrow x = {30^ \circ }\]
The angle \[x = {30^ \circ }\]
Then, the angle \[2x = 2 \times {30^ \circ }\]
Therefore, \[2x = {60^ \circ }\]
And
The angle \[3x = 3 \times {30^ \circ }\]
Therefore, \[3x = {90^ \circ }\]
Therefore, the angles in the ratio \[1:2:3\] are \[{30^ \circ }\] , \[{60^ \circ }\] and \[{90^ \circ }\] .
Therefore, the smallest angle of the triangle is \[{30^ \circ }\] .
And the largest angle of the triangle is \[{90^ \circ }\] .
Therefore, the difference between smallest and largest angle is \[{90^ \circ } - {30^ \circ } = {60^ \circ }\]

Hence, the difference between the smallest and largest angles of the triangle is \[{60^ \circ }\].

Note:
Angle sum property states that the sum of interior angles of a triangle is always \[{180^ \circ }\]. Also remember that if one angle of the triangle is \[{90^ \circ }\] then the other two angles will be acute angles. And the triangle with \[{90^ \circ }\] angle is called the right angled triangle.