Question

The angles of elevation of the top of a tower from two points at a distance of 4m and 9m from the base of the tower and in the same straight line with it are complementary. Prove that the height of the tower is 6m.

Answer 1

Hint: We draw a figure with respect to the data given in the question. Then we write down tan α and tan β. Use the relation (α + β = 90°) to solve.

Complete step-by-step answer:

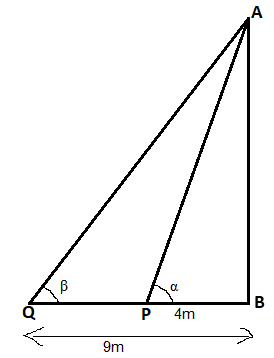
Let AB be the tower.

Let P and Q be the points at distance of 4m and 9m respectively.

From fig, PB = 4m, QB = 9m.

Let angle of elevation from P be α, and angle of elevation from Q be β.

Given that α and β are complementary. Thus, α + β = 90
(Two angles are complementary if their sum equals 90°.)

In triangle ∆ABP,
tan α = $\dfrac{{{\text{AB}}}}{{{\text{BP}}}}$ ………. (1)

In triangle ABQ,
tan β = $\dfrac{{{\text{AB}}}}{{{\text{BQ}}}}$

Now, tan (90 – α) = tan β = $\dfrac{{{\text{AB}}}}{{{\text{BQ}}}}$ (Since, α + β = 90)
⟹cot α = $\dfrac{{{\text{AB}}}}{{{\text{BQ}}}}$ (tan (90-θ) = cot θ) and tan θ = $\dfrac{1}{{\cot {\text{ }}\theta }}$

⟹$\dfrac{1}{{{\text{tan }}\alpha }}$ = $\dfrac{{{\text{AB}}}}{{{\text{BQ}}}}$
So, tan α = $\dfrac{{{\text{BQ}}}}{{{\text{AB}}}}$ …….. (2)

From (1) and (2)

$\dfrac{{{\text{AB}}}}{{{\text{BP}}}}$ = $\dfrac{{{\text{BQ}}}}{{{\text{AB}}}}$
⟹${\text{A}}{{\text{B}}^2}$ = BQ x BP

We know that, PB = 4m, QB = 9m.

⟹${\text{A}}{{\text{B}}^2}$ = 4 x 9

⟹${\text{A}}{{\text{B}}^2}$ = 36

Therefore, AB = 6.

Hence, the height of the tower is 6m.

Note: In order to solve this type of question the key is to draw an appropriate figure and establish the relation between what we want with what we have. Given angles are complementary is the biggest hint to break down the problem. Then we solve the relations for an answer.