Question

The angles of a triangle are \[2x\], \[3x\], and \[4x\] degrees. What is the value of \[x\]?

Answer 1

Hint: Given the angles of a triangle are \[2x\], \[3x\], and \[4x\] degrees. As we know, the sum of the measure of all the three angles in a triangle is \[180\] degrees. So, in this question, we will sum up all the three measures of the angle of the triangle and equate it to \[180\] degrees i.e., \[2x + 3x + 4x = 180\] and then we will simplify it to find the value of \[x\].

Complete step by step answer:
Given the angles of a triangle are \[2x\], \[3x\] and \[4x\] degrees, we have to find the value of \[x\].

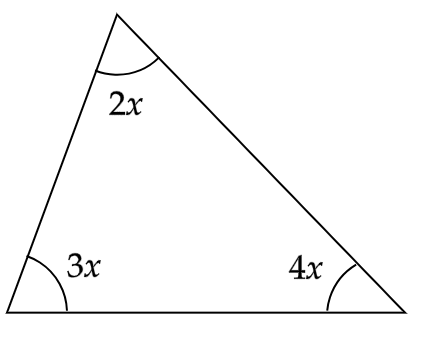
As we know, the sum of the measure of all the three angles in a triangle is \[180\] degrees.
On adding all the three measures of the angle of the triangle and equating it to \[180\] degrees, we get
\[ \Rightarrow 2x + 3x + 4x = 180\]
On simplification, we get
\[ \Rightarrow 9x = 180\]
On dividing both the sides of the equation by \[9\], we get
\[ \Rightarrow x = \dfrac{{180}}{9}\]
On calculating, we get
\[ \Rightarrow x = 20\]
Therefore, the value of \[x\] is \[20\].

Note:
Here, the question is of a triangle. Like the sum of the measures of the angles of a triangle having three sides is always \[{180^ \circ }\]. Similarly, the sum of the measure of the angles of a quadrilateral having four sides is always \[{360^ \circ }\], the sum of the measure of the angles of a pentagon having five sides is always \[{540^ \circ }\] and the sum of the measure of the angles of a hexagon having six sides is always \[{720^ \circ }\].