
The angle which makes a linear pair with an angle of \[61^\circ \] is of
A. \[29^\circ \]
B. \[61^\circ \]
C. \[122^\circ \]
D. \[119^\circ \]
Answer
478.8k+ views
Hint: In this problem first of all we will draw a rough diagram. We will approach this problem by using the definition of a linear pair of angles i.e., Linear pair of angles are formed when two lines intersect each other at a single point. In this problem, we have given one of the angles as \[61^\circ \] so we will let the other angle as \[x\] . Then we will use one of the properties of a linear pair of angles, that is the sum of angles of a linear always equal to \[180^\circ \] . After that we will substitute the values in the above conditions and simplify. Hence, we will get our required result.
Complete step by step answer:
Here, we have to find an angle which makes a linear pair with an angle of \[61^\circ \].Let the angle be \[x\]. Now we know that two angles are said to be a linear pair if they are adjacent. So, let’s draw a rough diagram,
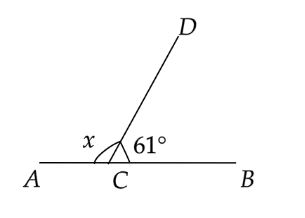
Now as we know, the sum of angles of a linear is always equal to \[180^\circ \]. Therefore, from the diagram,
\[\angle DCA + \angle DCB = 180^\circ \]
On substituting the values, we get
\[ \Rightarrow x + 61^\circ = 180^\circ \]
\[ \Rightarrow x = 180^\circ - 61^\circ \]
On subtracting, we get
\[ \therefore x = 119^\circ \]
Hence, the angle which makes a linear pair with an angle of \[61^\circ \] is of \[119^\circ \].
So, the correct answer is option D.
Note: As we know that the sum of angles of linear pair is always \[180^\circ \].
\[ \Rightarrow \angle DCA + \angle DCB = 119^\circ + 61^\circ = 180^\circ \]
In this way, we can check whether the solution is correct or wrong. Also sometimes many students get confused between adjacent angles and linear pairs. Adjacent angles are those that have a common vertex and common side but do not overlap while linear pairs are those that are adjacent, and the measure is \[180^\circ \] . So, don’t get confused between the two.Example of Linear Pair,
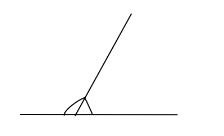
Example of Adjacent angle
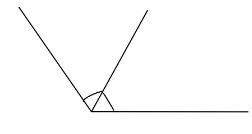
Complete step by step answer:
Here, we have to find an angle which makes a linear pair with an angle of \[61^\circ \].Let the angle be \[x\]. Now we know that two angles are said to be a linear pair if they are adjacent. So, let’s draw a rough diagram,

Now as we know, the sum of angles of a linear is always equal to \[180^\circ \]. Therefore, from the diagram,
\[\angle DCA + \angle DCB = 180^\circ \]
On substituting the values, we get
\[ \Rightarrow x + 61^\circ = 180^\circ \]
\[ \Rightarrow x = 180^\circ - 61^\circ \]
On subtracting, we get
\[ \therefore x = 119^\circ \]
Hence, the angle which makes a linear pair with an angle of \[61^\circ \] is of \[119^\circ \].
So, the correct answer is option D.
Note: As we know that the sum of angles of linear pair is always \[180^\circ \].
\[ \Rightarrow \angle DCA + \angle DCB = 119^\circ + 61^\circ = 180^\circ \]
In this way, we can check whether the solution is correct or wrong. Also sometimes many students get confused between adjacent angles and linear pairs. Adjacent angles are those that have a common vertex and common side but do not overlap while linear pairs are those that are adjacent, and the measure is \[180^\circ \] . So, don’t get confused between the two.Example of Linear Pair,

Example of Adjacent angle

Recently Updated Pages
Master Class 8 Social Science: Engaging Questions & Answers for Success

Master Class 8 English: Engaging Questions & Answers for Success

Class 8 Question and Answer - Your Ultimate Solutions Guide

Master Class 8 Maths: Engaging Questions & Answers for Success

Master Class 8 Science: Engaging Questions & Answers for Success

Master Class 9 General Knowledge: Engaging Questions & Answers for Success

Trending doubts
What is BLO What is the full form of BLO class 8 social science CBSE

Citizens of India can vote at the age of A 18 years class 8 social science CBSE

Full form of STD, ISD and PCO

Advantages and disadvantages of science

Right to vote is a AFundamental Right BFundamental class 8 social science CBSE

What are the 12 elements of nature class 8 chemistry CBSE





