Question

The angle substandard by and are at the centre is double the angle subtended by it at any point on the remaining part of the circle

Answer 1

Hint: An arc of a circle is any part of the circumference. The angle substandard by an at any point is the angle formed between the two line segments joining that point to the endpoints of the arc, In the following figure, an arc of a circle shown subtends an angle \[\alpha \] at a point on the
On the circumference, and an angle \[\beta \]at the center O.

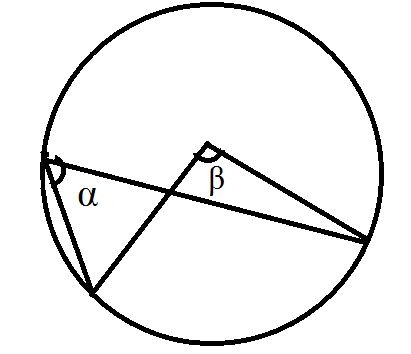
A central angle is an angle whose vertex is the centre O of a circle and whose legs (sides) are radio intersecting the circle in two distinct point A&B. Central angle are subtended by an arc between those two points, and the arc length is a (central) angles of a circle of radius one (measured in rations)
The length of an arc is simply the length of its portion of the circumference. The circumference itself can be considered a full circle are length are measure: In a circle, the degree measure of an arc is equal to the measure of the central angle that intercepts the arc.
Complete step by step answer:
A circle with the centre of at O
Are PQ of this circle subtending angles POQ at centre O & \[\angle PAQ\] at a point a remaining part of the circle.
To prove: - \[\angle POQ = 2\angle PAQ\] or. The angle subtended by an arc at the centre is double the angle subtended by it at any point on the remaining part of the circle

Construction: - There are two general cases:

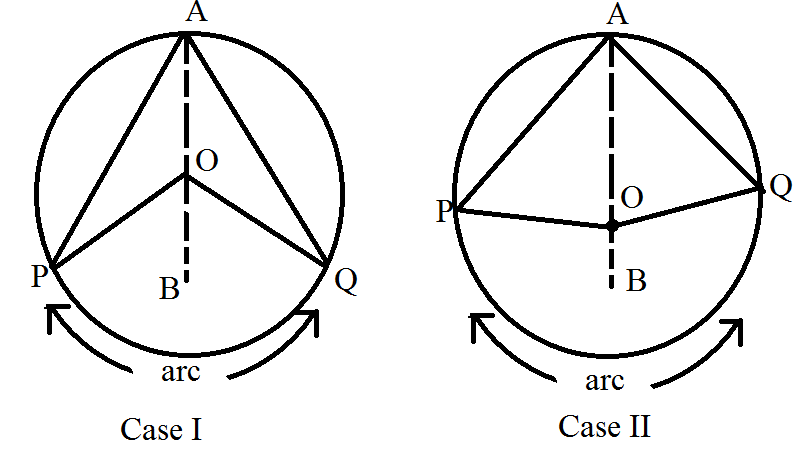
Case I- In \[\vartriangle APO\]
\[OP = OA\](Radius of a circle)
\[\angle OPA = \angle OAP\] (Angle opposite to equal sides are equal) _______(i)
Also by exterior angle property
\[ \Rightarrow \] Exterior angle is sum of interior opposite angle
\[\angle BOP = \angle OPA + \angle OAP\]
\[\angle BOP = \angle OAP + \angle OAP\]
\[\angle BOP = 2\angle OAP\]..........(ii)

Now IN \[\vartriangle AQO\]
\[OQ = OA\] (radius)
\[\angle OQA = \angle OAQ\] (angles opposite to equal sides are equal) _________(iii)
Also by exterior angle property
\[\therefore \]Exterior angle is sum of interior opposite angle
\[ \Rightarrow \angle BOQ = \angle OQA + \angle OAQ\]
Where \[\angle BOQ\] is exterior angle
\[\angle OQA\,\& \,\angle OAQ\] are interior angle
\[ \Rightarrow \angle BOQ = \angle OAQ + \angle OAQ\]
\[\angle BOQ = 2\angle OAQ\]
Adding equation (2) & (4)
\[ \Rightarrow \angle BOP + \angle BOQ = 2\angle OAP + 2\angle OAQ\]
\[ \Rightarrow \angle BOP + \angle BOQ = 2(OAP + 2\angle OAQ)\]
Where \[\angle BOP + \angle BOQ = \angle POQ\]
\[\angle OAP + \angle OAQ = \angle PAQ\]
\[ \Rightarrow \angle POQ = @\angle PAQ\]
Hence proved at the centre. The angle subtended by an \[\angle POQ\] is double the angle subtended by it at any point on the remaining part of the circle \[(\angle PAQ)\]

Note:
Case II
In \[\vartriangle APO\]
\[OP = OA\](Radius of a circle)
\[\angle OPA = \angle OAP\] (angle opposite to equal sides are equal) __________(i)
Also by exterior angle property
\[ \Rightarrow \] Exterior angle is sum of interior opposite angle
\[\angle BOP = \angle OPA + \angle OAP\]
\[\angle BOP = \angle OAP + \angle OAP\]
\[\angle BOP = 2\angle OAP\]..........(ii)
Again
In \[\vartriangle AQO\] (Similarly)
\[ \Rightarrow \angle BOQ = 2\angle OAQ\].... (3)
Adding equation (2) & (3)
\[\angle BOP + \angle BOQ = 2\angle OAP + 2\angle OAQ\]
\[\angle BOP + \angle BOQ = 2(OAP + \angle OAQ)\]

Where \[\angle BOP + \angle BOQ\]= reflex angle \[\angle POQ\]