Question

The angle of the minimum deviation of a $75{}^\circ$ prism of a dense glass is found to be $45{}^\circ$ when in air and $15{}^\circ$ when immersed in certain liquid. Then the refractive index of the liquid is:

$A.\sqrt{\dfrac{2}{3}}$
$B.\dfrac{3}{2}$
$C.\sqrt{\dfrac{3}{2}}$
$D.\sqrt{3}$

Answer 1

Hint: The angle of minimum deviation of the prism is found by the equation:
${{\mu }_{12}}=\dfrac{\sin \dfrac{A+D}{2}}{\sin \dfrac{A}{2}}$
Where A is the angle of the prism, D is the angle of deviation. This equation is helpful in finding the answer for this question.

Complete answer:
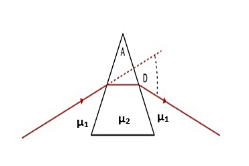
First of all let us take a look at the angle of minimum deviation. Angle of minimum deviation is defined as the smallest angle at which light is bent by an optical instrument or a system like a lens. The angle of deviation is minimum if the incident and refracted rays are forming equal angles with the faces of prism. The angle is having very much importance which is relative to prism spectroscopes since it can be determined easily.

Here in this question, it is mentioned that angle of prism is
${{D}_{2}}=15{}^\circ $ $A=75{}^\circ $
Angle of minimum deviation in air is
${{D}_{1}}=45{}^\circ $
And angle of minimum deviation in a liquid is given as
${{D}_{2}}=15{}^\circ $
As we all know the refractive index of a prism is given as
${{\mu }_{12}}=\dfrac{\sin \dfrac{A+D}{2}}{\sin \dfrac{A}{2}}$
Refractive index of air is
${{\mu }_{air}}=1$
Refractive index of that liquid be n.
Taking the ratio between this two will be
$\sqrt{\dfrac{3}{2}}=1.2247$ $\dfrac{{{\mu }_{1}}}{n}=\dfrac{\dfrac{\sin \left( \dfrac{A+{{D}_{1}}}{2} \right)}{\sin \dfrac{A}{2}}}{\dfrac{\sin \left( \dfrac{A+{{D}_{2}}}{2} \right)}{\sin \dfrac{A}{2}}}$
Both the denominators are the same,
Therefore we can write that
$\dfrac{1}{n}=\dfrac{\sin \left( \dfrac{A+{{D}_{1}}}{2} \right)}{\sin \left( \dfrac{A+{{D}_{2}}}{2} \right)}$
Substituting the values in this will give,
$\dfrac{1}{n}=\dfrac{\sin \left( \dfrac{75+45}{2} \right)}{\sin \left( \dfrac{75+15}{2} \right)}$
It will be written as,

$\dfrac{1}{n}=\dfrac{1.423}{1.162}$
Therefore refractive index of the certain liquid is
$n=1.225$
$\sqrt{\dfrac{3}{2}}=1.2247$

So, the correct answer is “Option C”.

Note:
Refractive indexes are dimensionless quantities. There will be no units for this as it is a constant.
Refractive index of a material is actually meant by how much speedily light can travel through a specific media.