Question

The angle of some triangles is given below. Classify each triangle acute-angled, obtuse-angled, or right-angled on the basis of its angles.
A) $90^\circ$, $45^\circ$, $45^\circ$
B) $60^\circ$, $60^\circ$, $60^\circ$
C) $80^\circ$, $60^\circ$, $40^\circ$
D) $92^\circ$, $50^\circ$, $38^\circ$
E) $120^\circ$, $50^\circ$, $10^\circ$
F) $90^\circ$, $35^\circ$, $55^\circ$

Answer 1

Hint: When one angle of a triangle is equal to the $90^\circ $, it is a right-angled triangle. When all three angles are less than $90^\circ $, it is an acute-angled triangle. When one angle of a triangle is greater than $90^\circ $, it is an obtuse angled triangle.

Complete step-by-step answer:
For part (a),

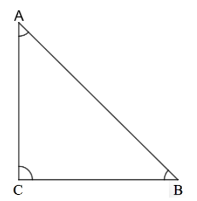
In this triangle, we have an angle equal to $90^\circ$ and others are less than $90^\circ$.
Thus, it is a right-angled triangle.
For part (b),

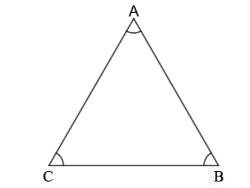
In this triangle, we have all angles less than $90^\circ$.
Thus, it is an acute-angled triangle.
For part (c),

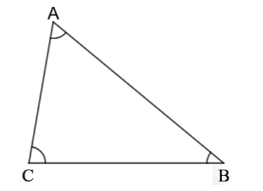
In this triangle, we have all angles less than $90^\circ$.
Thus, it is an acute-angled triangle.
For part (d),

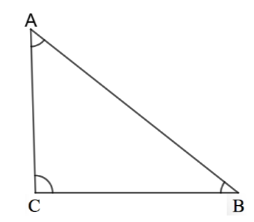
In this triangle, we have an angle greater than $90^\circ$ and others are less than $90^\circ$.
Thus, it is an obtuse-angled triangle.
For part (e),

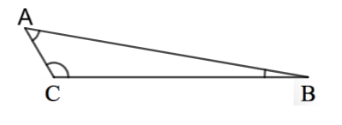
In this triangle, we have an angle greater than $90^\circ$ and others are less than $90^\circ$.
Thus, it is an obtuse-angled triangle.
For part (f),

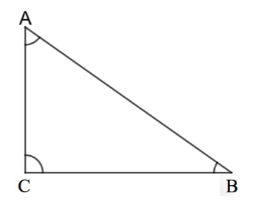
In this triangle, we have an angle equal to $90^\circ$ and others are less than $90^\circ$.
Thus, it is a right-angled triangle.

Note: A “triangle” is a three-sided polygon having three angles. The sum of all interior angles of a triangle will always add up to 180 degrees. This property is called the angle sum property.
The sum of all the internal angles of a triangle is always $180^\circ$ no matter how the triangle is constructed.
The length of any side of a triangle is shorter than the sum of the other two sides.
A triangle can always be split into two right triangles no matter how the triangle is constructed.