Question

The angle of elevation to the top of the building in Brisbane is found to be ${6^ \circ }$ from the ground at a distance of 1 km from the base of the building. Using this information, I need to find the height of the building to the nearest tenth of a metre. How?

Answer 1

Hint: This is a problem based on applications of trigonometry. Here the angle of elevation is given i.e. ${6^ \circ }$. The ground distance is also given. We need to find the height of the building. Here we will use the one of the trigonometric ratios formula to find the height of the building.

Complete step-by-step answer:
Now let’s find the value of ${6^ \circ }$in radian:
We know that $\pi $ radians is equal to \[{180^ \circ }\]
Now the value of ${1^ \circ }$ in radian $ = \dfrac{\pi }{{{{180}^ \circ }}}$
So the value of ${6^ \circ }$ in radian $ = \dfrac{{6\pi }}{{{{180}^ \circ }}}$
${6^ \circ } = 0.104719$radians
Now as the value of ${6^ \circ }$in radian ($0.104719$)tends to zero we know that:
$\mathop {\lim }\limits_{\theta \to 0} \tan \theta = \theta $; ($\theta $ is in radians)
$\tan {6^ \circ } = \tan \left( {0.104719} \right) = 0.104719$
In the given figure the distance from the base of the building is 1000 metres and we need to find the height of the building.

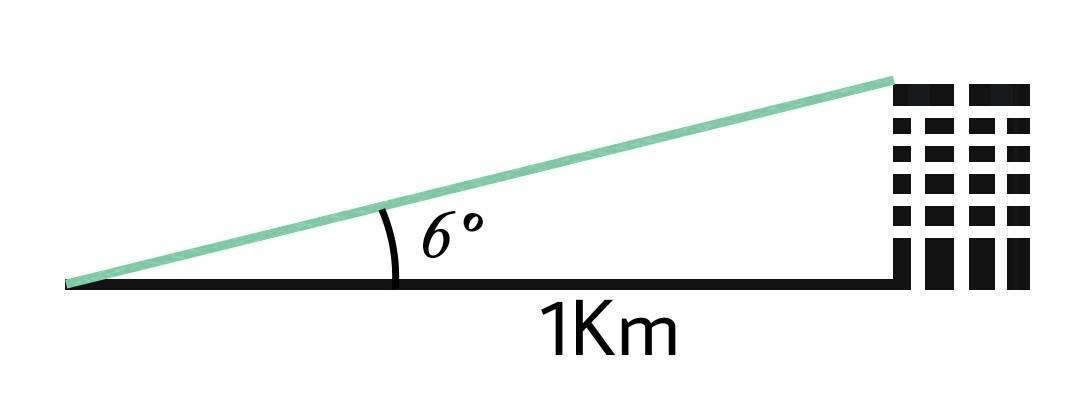
Since we have the value of $\tan {6^ \circ }$ and we know the length of the base ($1000m$)we just need to find the perpendicular (height of building).
$\tan \theta = \dfrac{{perpendicular}}{{base}}$
Now let’s substitute the values $\theta = {6^ \circ }$and base $ = 1000m$
$\tan {6^ \circ } = \dfrac{{perpendicular}}{{1000m}}$
$0.104719 = \dfrac{{perpendicular}}{{1000m}}$
Perpendicular $ = 0.104719 \times 1000m$
Perpendicular $ = 104.719m$
Perpendicular $ = 104.7m$nearest to tenth of a metre
The height is found to be 104.7 metres (nearest to tenth of a metre)

Note: Sometimes you can get some differences in the values of sine and tangent of the angle (especially in the third and fourth decimal places), but that extent of error is acceptable if the exact values are not given.