Question

The angle of elevation of tower of height h standing inside a triangular field at each corner is $60{}^\circ $ . If the length of the sides of the field are 30 m, 50 m and 70 m, then find the value of ${{h}^{2}}+h+1$ .

Answer 1

Hint: Firstly, draw the figure with the given conditions. Then, find the value of the triangular field using Heron’s formula which is given by $\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ , where s is the semi-perimeter of the triangle which is given by $s=\dfrac{a+b+c}{2}$ and a, b and c are the sides of the triangle. Then find the circumradius, R using the formula $R=\dfrac{abc}{4\Delta }$ . Using the definition of $\tan \theta $ , that is, $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$ , the value of h can be found. Substitute this value of h in ${{h}^{2}}+h+1$ and simplify.

Complete step by step answer:
Let us illustrate the given situation. From the below figure, we can see that the triangular field is ABC on which a tower PQ of length h m is standing. $\angle PBQ=\angle PCQ=60{}^\circ $

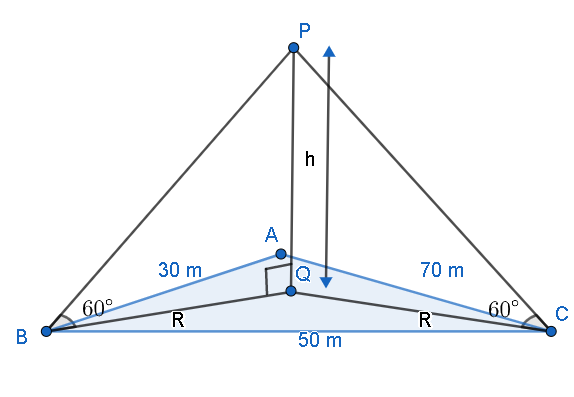
Let us consider $AB=30\text{m},BC=50\text{m and }AC=70\text{m}$ .
We have to find the value of h so that the value of ${{h}^{2}}+h+1$ can be found. Let us find the area of triangle ABC using Heron’s formula.
We know that according to Heron’s formula, the area of a triangle of sides a, b and c is given by
$\Delta =\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$
where s is the semi-perimeter of the triangle which is given by
$s=\dfrac{a+b+c}{2}$
Let us substitute $a=30m,b=50m\text{ and }c=70m$ in the above formulas.
$\begin{align}
  & \Rightarrow s=\dfrac{30+50+70}{2} \\
 & \Rightarrow s=\dfrac{150}{2} \\
 & \Rightarrow s=75\text{ m} \\
\end{align}$
Now, let us find the area of triangle ABC.

$\begin{align}
  & \Delta =\sqrt{75\left( 75-30 \right)\left( 75-50 \right)\left( 75-70 \right)} \\
 & \Delta =\sqrt{75\times 45\times 25\times 5} \\
 & \Delta =\sqrt{421875} \\
 & \Delta =375\sqrt{3}\text{ }{{\text{m}}^{2}} \\
\end{align}$
Let R be the circumradius of the triangle which is given by the formula
$R=\dfrac{abc}{4\Delta }$
where a, b and c are the sides of a triangle and $\Delta $ is the its area.
\[\begin{align}
  & \Rightarrow R=\dfrac{30\times 50\times 70}{4\times 375\sqrt{3}} \\
 & \Rightarrow R=\dfrac{70}{\sqrt{3}}\text{ m} \\
\end{align}\]
From the figure, we can see that triangle PBQ is a right-angled triangle. Therefore,
$\begin{align}
  & \tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}} \\
 & \Rightarrow \tan 60{}^\circ =\dfrac{h}{R} \\
 & \Rightarrow \sqrt{3}=\dfrac{h}{\dfrac{70}{\sqrt{3}}} \\
 & \Rightarrow h=70\text{ m} \\
\end{align}$
Now, let us find ${{h}^{2}}+h+1$ .
$\begin{align}
  & \Rightarrow {{h}^{2}}+h+1={{70}^{2}}+70+1 \\
 & \Rightarrow {{h}^{2}}+h+1=4900+71 \\
 & \Rightarrow {{h}^{2}}+h+1=4971 \\
\end{align}$
Hence, the value of ${{h}^{2}}+h+1$ is 4971.

Note: Students must be able to draw the figure with the given conditions carefully. They have a chance of making a mistake by writing the Heron’s formula as $\Delta =\sqrt{s\left( s+a \right)\left( s+b \right)\left( s+c \right)}$ . Students have a chance of making a mistake by considering $\angle PBC$ as $60{}^\circ $ .