Question

The angle of elevation of the top of the tower as observed from a point in the horizontal plane through the foot of the tower is $32{}^\circ .$ When the observer moves towards the tower a distance 100m, he finds the angle of elevation of the top to be $63{}^\circ .$ Find the height of the tower and the distance of the first position from the foot of the tower.

Answer 1

Hint: Assume that the height of the tower is h. Using $\tan \alpha =\dfrac{AB}{AD}$, find the length AD in terms of h.
Using $\tan \beta =\dfrac{AB}{AC}$ form an equation in h and hence find the value of h. Using the expression of AD in terms of h find the length AD. Hence find the distance of point C from A.

Complete step-by-step answer:

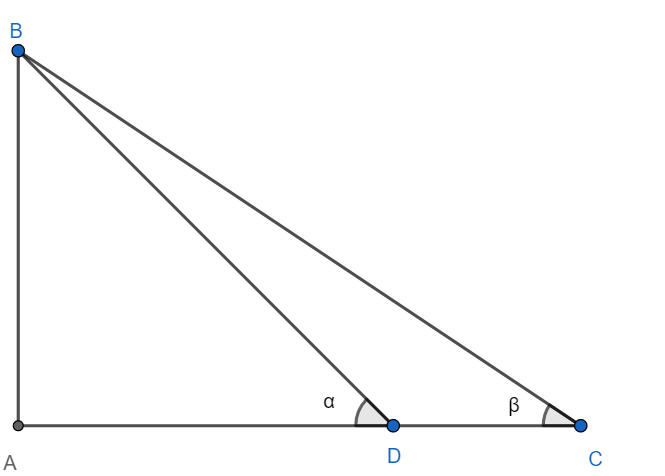
Given: AB is a tower. The angle of elevation of the tower from point C is $\beta =32{}^\circ $ , and the angle of elevation of the tower from point D is $\alpha =63{}^\circ $. DC = 100m.
To determine: The height of the tower AB and the distance of C from the foot of the tower.
Let the height of the tower be h. Hence, we have AB = h.
We have in triangle ABD, AB is the side opposite to $\alpha $ , and AD is the side adjacent to $\alpha $.
We know that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
Hence, we have $\tan \alpha =\dfrac{AB}{AD}$
Multiplying both sides by $\dfrac{AD}{\tan \alpha },$ we get
$AD=\dfrac{h}{\tan \alpha }\text{ (i)}$
Also, in triangle ABC, AB is the side opposite to $\beta $ and AC is the side adjacent to $\beta $.
We know that $\tan \theta =\dfrac{\text{Opposite side}}{\text{Adjacent side}}$
Hence, we have $\tan \beta =\dfrac{AB}{AC}$
Multiplying both sides by AC, we get
$AB=AC\tan \beta $
Also, we have AC = AD +DC
Substituting the value of AD from equation (i) and substituting DC = 100, we get
$h=\left( \dfrac{h}{\tan \alpha }+100 \right)\tan \beta $
Hence, we have
$h=\dfrac{h\tan \beta }{\tan \alpha }+100\tan \beta $
Subtracting $\dfrac{h\tan \beta }{\tan \alpha }$ from both sides of the equation, we get
$h-\dfrac{h\tan \beta }{\tan \alpha }=100\tan \beta $
Taking $h$ common from the terms on LHS, we get
$h\left( 1-\dfrac{\tan \beta }{\tan \alpha } \right)=100\tan \beta $
Dividing both sides of the equation by $1-\dfrac{\tan \beta }{\tan \alpha }$, we get
$h=\dfrac{100\tan \beta }{1-\dfrac{\tan \beta }{\tan \alpha }}$
Substituting $\tan \beta =\tan 32{}^\circ =0.6248$ and $\tan \alpha =\tan 63{}^\circ =1.9626$, we get
$h=\dfrac{100\left( 0.6248 \right)}{1-\dfrac{0.6248}{1.9626}}=91.67$
Hence, we have h = 91.67m
Hence the height of the tower is 91.67m.
Substituting the value of h in the equation (i), we get
$AD=\dfrac{h}{\tan \alpha }=\dfrac{91.67}{1.9626}=46.7$
Hence, we have AC = AD + DC = 46.7+100 = 146.7m.
Hence the distance of the first point of observation from the foot of the tower is 146.7 m.

Note: Verification:
We have AB = 91.67m, AD = 46.7m
Hence, we have $\dfrac{AB}{AD}=\dfrac{91.67}{46.7}=1.9629=\tan 63{}^\circ $
Hence $\alpha =63{}^\circ $
Also, AB = 91.67m and AC = 146.7m
Hence, we have $\dfrac{AB}{AC}=\dfrac{91.67}{146.7}=0.6248=\tan 32{}^\circ $
Hence, we have $\beta =32{}^\circ $
Hence our solution is verified to be correct.