Question

The angle of elevation of the top of a tower from a point A on the ground is 30. On moving a distance of 20 meters towards the foot of the tower to a point B the angle of elevation increases to 60. Find the height of the tower and the distance of the tower from the point A.

Answer 1

Hint: Here, we will first draw the triangle using the given condition to simplify the calculation. Then we will use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base in triangle with angles 30 degrees and 60 degrees, separately to find the value of \[h\]. Then we will substitute the value of \[h\] to find the distance of the tower from the point A.

Complete step by step solution:
We are given that the angle of elevation of the top of a tower from a point A on the ground is 30 and on moving a distance of 20 meters towards the foot of the tower to a point B the angle of elevation increases to 60.
Let us assume that the height of the tower DC is \[h\] and the length AC is \[d\].
First, we will draw the triangle using the given conditions.

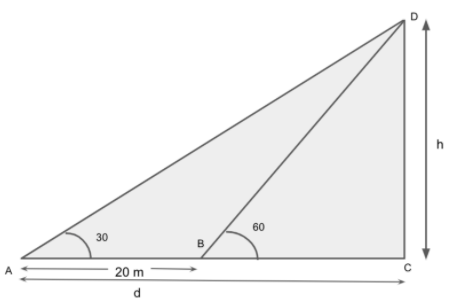
We will first take the triangle \[\Delta {\text{ACD}}\],

We will use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base.

Using the above tangential property, we get

\[\tan 30^\circ = \dfrac{{{\text{DC}}}}{{{\text{AC}}}}\]

Substituting the values of the length AC and DC in the above equation, we get

\[
  \tan 30^\circ = \dfrac{h}{d} \\
  \dfrac{1}{{\sqrt 3 }} = \dfrac{h}{d} \\
 \]

Cross-multiplying the above equation, we get

\[d = \sqrt 3 h{\text{ ......}}\left( 1 \right)\]

We will now take the triangle \[\Delta {\text{BCD}}\],

We will use the tangential property, that is, \[\tan {\text{A}} = \dfrac{p}{b}\], where \[p\] is the perpendicular and \[b\] is the base.

Using the above tangential property, we get

\[\tan 60^\circ = \dfrac{{{\text{DC}}}}{{{\text{BC}}}}\]

Substituting the values of the length AC and BC in the above equation, we get

\[
  \tan 60^\circ = \dfrac{h}{{d - 20}} \\
  \sqrt 3 = \dfrac{h}{{d - 20}} \\
 \]

Cross-multiplying the above equation, we get

\[\sqrt 3 \left( {d - 20} \right) = h{\text{ ......}}\left( 2 \right)\]

From equation \[\left( 1 \right)\] and equation \[\left( 2 \right)\], we get
\[
   \Rightarrow \sqrt 3 \left( {\sqrt 3 h - 20} \right) = h \\
   \Rightarrow 3h - 20\sqrt 3 = h \\
 \]

Subtracting the above equation by \[h\] on both sides, we get

\[
   \Rightarrow 3h - h - 20\sqrt 3 = 0 \\
   \Rightarrow 2h - 20\sqrt 3 = 0 \\
 \]

Adding the above equation with \[20\sqrt 3 \] on both sides, we get

\[
   \Rightarrow 2h - 20\sqrt 3 + 20\sqrt 3 = 0 + 20\sqrt 3 \\
   \Rightarrow 2h = 20\sqrt 3 \\
 \]

Dividing the above equation into both sides by 2, we get

\[
   \Rightarrow \dfrac{{2h}}{2} = \dfrac{{20\sqrt 3 }}{2} \\
   \Rightarrow h = 10\sqrt 3 \\
 \]

Thus, the height of the tower is \[10\sqrt 3 \] meters.

Substituting the above value of height of the tower in equation \[\left( 1 \right)\], we get

\[
   \Rightarrow d = \sqrt 3 \times 10\sqrt 3 \\
   \Rightarrow d = 10 \times 3 \\
   \Rightarrow d = 30 \\
 \]

Therefore, the distance from the foot of the tower to point A is 30 meters.

Note:
In solving these types of questions, you should be familiar with the concept of angle of elevation and the tangential properties. Students should make the diagram for better understanding. Using the values of respective angles you can simply find any length present in the figure using the tangential value ‘\[\tan \]’, which makes our problem easy to solve. We will multiply the root number with itself is equal to the number. For example, the product of \[\sqrt 3 \] with itself is 3.