Question

The angle of elevation of the top of a tower at a distance of \[500m\] from its foot is 30 degrees. The height of the tower is?

Answer 1

Hint: This is a question of Trigonometry from the Height and Distance section. To solve this we will use a formula of trigonometric identity applicable in a right angle triangle. Here first we should observe which trigonometric identity we can use here , suppose if we have perpendicular and base then we will use $ \tan $ , if we have perpendicular and hypotenuse then we will use $ \sin $ , if we have base and hypotenuse then we will use $ \cos $ . Since here we have base and one angle and we have to find perpendicular so our best option is to use $ \tan $
Suppose in a right angle triangle if one angle is $ \alpha $ other than right angle.
Then we know formula of

Complete step-by-step answer:
Let’s assume height of the tower $ AB $ is $ x $ meter which is perpendicular of triangle $ ABC $ distance between point $ A $ and $ C $ is $ 500 $ meter which is the base of triangle $ ABC $

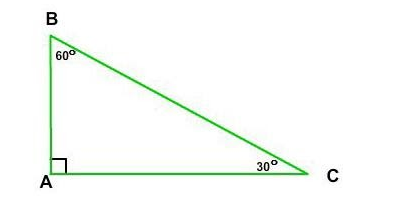
Here, AB represents the height of the tower and AC is horizontal distance.
We have to find value of $ AB $
 $ \tan 30=\dfrac{AB}{AC} $
Put the value of $ AC $
 $ \dfrac{1}{\sqrt{3}}=\dfrac{AB}{500} $
 $ 500=AB\times \sqrt{3} $
 $ \dfrac{500}{\sqrt{3}}=AB $
 $ AB=288.67m $
Height of tower is $ AB=288.67m $

Note: To solve this question we should have knowledge of trigonometric identity and their formulas, we should know which trigonometric identity is applicable here among all six. We should know the concept of elevation and depression angles too. If we are looking at something from downward to upward then our eyes make an elevation angle but if we are looking from upward to downward then our eyes make a depressed angle.